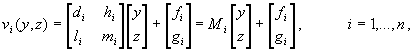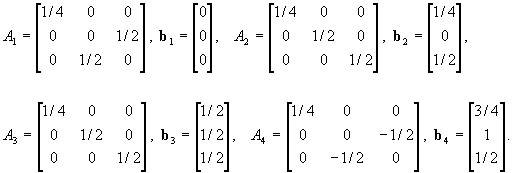|
3. Block diagonal IFS Nevertheless, under feasible conditions, by carefully choosing the IFS the parametric curve { f(t) = [f(t) y(t)]T, t ÎI} can be built so to have the property of self-affine planar interpolating curves, which is characteristic of most classical well known fractal curves such as the Peano square (1890), the von Koch snowflake (1906) or the Sierpinski triangle (1915). Among these the Peano or space filling curves are especially interesting : these are curves whose graph is identical to a nonempty pathwise connected compact subset of R 2 (Barnsley [3], p. 240), and find interesting applications in computer graphics, see for example [15]. The construction is as follows. Suppose that the data set from the (y, z)-plane
Dyz
= {Qi = [ yi zi]T,
i
= 0, 1,..., n} (n ³
2)
is given, satisfying
Given a polygonal line L with vertices {[pj
qj]T, j =
0, 1, ..., m} (m ³ 2), such
that [p0 q0]T
= [ y0 z0]T
=
Q0
and [pm qm]T
= [ yn zn]T =
Qn
,
one can build a set of affine mappings { vi :
R
2®
R
2,
i
= 1,..., n}, having the form
and satisfying the four interpolation conditions
Let t(Dyz) = {R2; v1,..., vn} be the IFS connected to the transformations (10). It follows from (11) that for fixed i , two out of six parameters di, hi, li, mi, fi, gi are free. For the reason of convenience, one may suppose that these free parameters are items of the matrix Mi. So, the set of matrices M = {Mi, i = 1,.., n} appears as the parameter of the IFS t(Dyz) and this fact will be stressed by the notation t(Dyz,M). If the elements of Mi for all i = 1,.., n satisfy conditions (7a) or (7b), it follows from the proof of Lemma 1 that r(Mi) < 1, and the IFS t(Dyz) is hyperbolic. Definition 1. Given the mesh Dx = {x0< x1< ...< xn } and the data set Dyz = {Qi = [ yi zi]T, i = 0,..,n}, we call D = { [xi yi zi]T , i = 0, 1,..., n} a lifting of Dyz on Dx. Let t(Dyz,M) be an IFS built as above and let D be a lifting of Dyz on Dx. Then, we call the IFS s(D) = s(D,M) built according to Theorem 1, a lifting of t(D) = t(Dyz,M) on Dx. The following theorem then holds. Theorem 2. If the IFS t(Dyz,M) is hyperbolic, then its lifting s(D,M) is also hyperbolic. Moreover, the attractor of t(Dyz,M) is the orthogonal projection of the attractor of s(D,M) onto the (y, z)-plane. It has self-affine structure and interpolates the data set Dyz . Proof. For every i = 1,..., n, (10) and (11) above yield yi - yi-1- di(yn -y0) - hi(zn -z0) = 0 and zi - zi-1- li(yn -y0) - mi(zn -z0) = 0 , which, in connection with the hypothesis that s(D,M) is the lifting of t(Dyz,M), gives ci= 0 and ki = 0 according to the formulas in Theorem 1. Furthermore, under these hypotheses, the expressions for the known terms fi and gi from Theorem 1 are consistent with (11). This means that every transformation wi splits into two independent components wi(P) = [ui(x) vi(y, z)]T, the first one being the contraction of the real line ui(x) = ai x + ei, and the second one, acting in the (y, z)-plane, being just vi(y, z). Now, if the IFS t(Dyz,M) is hyperbolic, r(Mi) < 1 holds for every i, and therefore r(Ai) = max{|ai|, r(Mi)}< 1 also holds for i = 1,..., n, and s(D,M) is hyperbolic, too. Let F and F denote the attractors of s(D,M) and t(Dyz,M) respectively. Let Fx and Fyz respectively denote projections of F on x-axis and yz-plane. Let Fi = wi(F) and let (Fi)yz be the yz-projection of Fi . Then, by the block diagonal structure of wi it follows that wi(F) = Fi = [ui(Fx) vi(Fyz)]T or, vi(Fyz) = (Fi)yz . Also, ÈiFi = F implies Èi(Fi)yz = Fyz, which is equivalent to Èi vi(Fyz) = Fyz . So, Fyz is the fixed point of the Hutchinson operator Èi vi( . ) and the (unique) attractor of t(Dyz,M). Accordingly, F = Fyz and Fyz is a self-affine set. It is straightforward to see, from (11), that Dyz Ì Fyz i.e., the attarctor of t(Dyz,M) interpolates the data set Dyz . à As far as the matter of supplying two extra conditions to (11) that will define the remaining parameters of transformation vi, according to the literature, there are two ways. The first one ([2]) uses n prescribed points in the (y, z)-plane, {Ri, i = 1,..., n} and demands that vi(pj, qj) =Ri, (j¹0,m), i = 1,..., n. In this way, the configuration of the points {Ri} influences the shape of the sequence of preattractors and the attractor itself. The second method reduces the number of parameters of vi to four by demanding that {vi} belong to some subset of the set of affine planar mappings like in the case of Peano or space filling curves [12]. Example 2 (Space-filling curve). Let Dyz = {(0, 0), (0, 1/2), (1/2, 1/2), (1, 1/2), (1, 0)}, and let L= {(0, 0), (0, 1/2), (1/2, 1), (1, 1/2), (1, 0)}. The mappings v1, v2, v3 and v4 determined by (11) and by v1,4(1/2, 1)=(1/2, 1/4), v2(1/2, 1)=(1/4, 1), v3(1/2, 1)=(3/4, 1) define the hyperbolic IFS t(Dyz). Choice of the mesh {xi}={0, 1/4, 1/2, 3/4, 1} leeds to the lifted IFS s(D) ={R3; w1, w2, w3, w4} where the matrix coefficients of w1, w2, w3 and w4 are
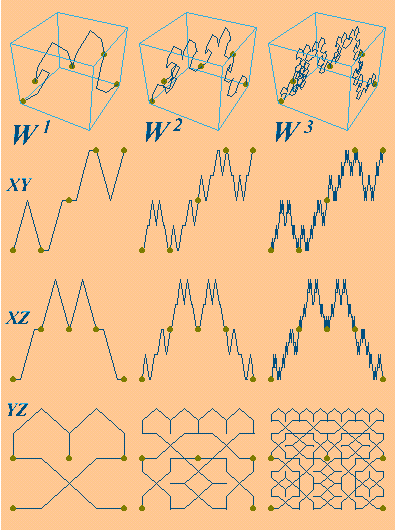
The first three iterations W 1, W 2 and W 3 of the Hutchinson operator W associated with s(D), applied to L, are shown in Figure 3 (top) along with the corresponding projections on the coordinate planes. The yz-projections of W1(L), W 2(L) and W 3(L) are successive approximations of Fyz , the yz-projection of the attractor F of s(D). These self-affine continuous curves being contained in the unit square [0, 1]2 suggest that F is also a continuous curve, it has self-affine structure and it "fills" [0, 1]2 .
Figure 3. The vector-valued fractal interpolation function containing a self-affine Peano curve as a component . |