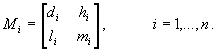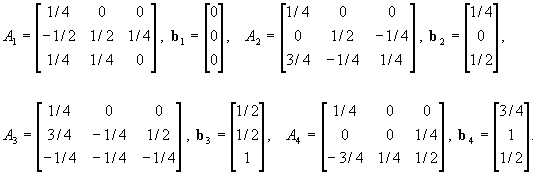|
The following theorem supplies the basic elements necessary for construction of generalized fractal interpolation functions. Theorem 1. Let the interpolating data set D = {Pi = [xi yi zi]T Î R3, xi < xi+1, i = 0, 1,.., n}(n ³ 2) be given. Consider the IFS s(D) = {R 3; w1,..., wn}, where wi are given by (1) with
and the real numbers di, hi, li, mi are parameters chosen such that wi (i = 1,..., n ) are contractive mappings. Then, the limiting set FD= limk ®¥W k( G ), is the graph of a continuous vector valued function f : [x0, xn] ® R2 having the interpolation property f(xi) = [ yi zi]T , i = 0,1,..., n. Proof. It is straightforward
to see that, with the special choice of ei,
fi, gi given here, the transformations
in the IFS take the form
For i = 1,..,n, denote by Mi the
sub-matrix of Ai whose elements are di,
hi, li, mi
The conditions that di, hi, li, mi must obey in order that a transformation of the form of wi Îs(D) be a contraction, are given in the following lemma. Lemma 1.
A transformation wi having
the form (1)with
ai <
1
is a contraction of R3 if
and only if the elements di, hi,
li, mi of Ai
satisfy
one of the following two systems of inequalities
Proof. Denote
the
spectral radius of a matrix M by r(M).
Then
is a necessary and sufficient condition for the mapping wi to be a contraction w.r.t. a feasible metric d in R 3. Let Qi = (di-mi)2 + 4 hi li , and let l1(i) , l2(i) , l3(i) denote the eigenvalues of the matrix Ai in (2), more precisely let l1 (i) = ai, l2(i)= 1/2( di+ mi - ÖQi ) and l3(i)= 1/2( di+ mi+ ÖQi). Then, (8) is equivalent to | lk(i)| < 1, k = 1, 2, 3 Let Qi ³ 0 ( this is equivalent to the first inequality in the first system in the assertion ). Then, l2(i) , l3(i) Î R, and l2(i) £ l3(i).So the condition {|l2(i)| < 1 Ù |l3(i)| < 1 } is equivalent to { -1 < l2(i) Ù l3(i) < 1 }, or {ÖQi < di + mi + 2 Ù ÖQi < -di-mi + 2} which, in turn, is equivalent to the set of inequalities ÖQi < 2 - di- mi , di+ mi ³ 0, ÖQi < 2 + di+ mi , di+ mi < 0. By squaring both sides of both left inequalities and replacing Qi = (di-mi)2 + 4 hi li, the above set reduces to the second inequality of (7a). If, instead, Qi < 0, the first inequality in the second system is satisfied. Furthermore, in this case l2(i) and l3(i) are conjugate complex numbers having common modulus |l2(i)| = |l3(i)| = 1/2| di + mi + i Ö(-Qi )| = 1/2 Ö[(di+mi)2- Qi ], therefore the condition {|l2(i)| < 1 Ù |l3(i)| < 1} yields Ö[ (di+mi)2- Qi ] < 2 which reduces to Ö(dimi-hi li) < 1, and to the second inequality of (7b), which is thereby completely proved. à The folowing corollary gives the condition on matrices Mi ( i = 1,..,n) under which the IFS is hyperbolic. Corollary 1. The IFS s(D) = {R3; w1, ..., wn}, built according to the rules given in Theorem 1, is hyperbolic if and only if for all i = 1,..., n the elements of the parameter matrix Mi satisfy the conditions (7a) and (7b). Proof. It is straightforward since the hypotheses made in Theorem 1 about D yield ai < 1 ( i = 1,.. ,n) and, therefore, Lemma 1 applies. à Let us denote by M the set of all the parameter matrices in the IFS s(D), M = {Mi, i = 1,..,n}. It is clear, now, that the uniqueness of the attractor of s(D) and, of course, the shape of the attractor itself depend on the parameter matrices M just as well as on the interpolation data D. Therefore, in the following, whenever this dependence will be relevant to our discussion we will introduce the set of parameter matrices in our notation, denoting by s(D,M) the corresponding IFS. Also we will denote by the same symbol the corresponding interpolation scheme, namely the rule by which the continuous vector valued function f , being the unique attractor of s(D,M), is associated to D. Example 1. Consider the data set D= {(0, 0, 0), (1/4, 0, 1/2), (1/2, 1/2, 1), (3/4, 1, 1/2), (1, 1, 0)}. By Theorem 1, a four term IFS s(D) = {R 3; w1, w2, w3, w4}, such that its attractor is the graph of a vector valued fractal interpolation function f, can be associated to D. If the items of {Mi , i = 1,..,4} are chosen, for example, to be : d1 = d2= 1/2, d3 = -1/4, d4 = 0; h1 = h4 = 1/4, h2 = -1/4, h3 = 1/2; l1 = l4 = 1/4, l2 = l3 = -1/4; m1 = 0, m2 = 1/4, m3 = -1/4, m4 =1/2, then the affine mappings w1, w2, w3, w4 have the form (2), with
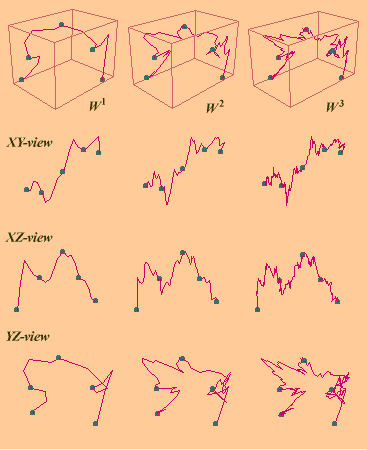
Direct checking shows that this choice of di, hi, li, mi satisfies constraints in Lemma 1, so the coefficient matrices above define contractive linear mappings R 3® R 3. Indeed, one could also evaluate directly r( A1) = r( A4) = (1+ Ö2 )/4 » 0.603553, r(A2) = ( 3 + Ö5 )/8 » 0.654508, and r(A3) = Ö3 /4 » 0.433013, to discover that all are smaller than 1, which guarantees that the IFS s(D) is hyperbolic and its attractor FD is unique. In Figure 1 (top) the preattractors W 1(G), W 2(G) and W 3(G) are displayed, where G is the piecewise linear interpolant of D. The rest of Fig. 1 shows the projections of these preattractors on the coordinate planes. The interpolating points are marked in all projections.
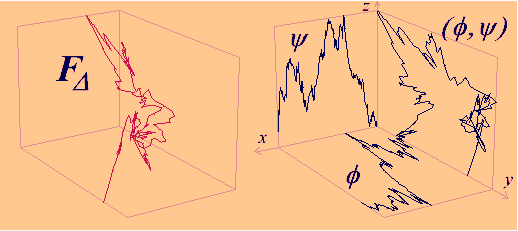
Figure 1. Preattractors of FD and their projections on the coordinate planes Figure 2 (left) shows the attractor of the orbit of G, this is FD = {[x f(x) y(x)]T, x ÎI= [0,1]} which is the graph of f (x) = [f(x) y(x)]T . The projections of FD on the coordinate planes, f ={ [x f(x)]T, xÎI}, y={[x y(x)]T, xÎI}and the parametric curve f = (f,y) are shown in Figure 2 (right). The functions f and y are called hidden variable fractal interpolation functions (Barnsley [2], [3], Massopust [14]) meaning that they depend on the "third variable" that is not present in the plane containing their graphs. In fact they do share the interpolation property of FDbut, while FD is, by its own nature, a self affine set, in the general case the projections f and y are not self affine.
Figure 2. Components of f . |