| Problems
in a Digital Description of
a Configuration of Atoms and Some Other Geometrical Topics in Physics T.
Ogawa
Institute of
Applied Physics,
This
paper is based on my two separate talks at the symposium, but not a simple
combination of them. Their titles are "WHAT CAN BE SEEN FROM THE VORONOI-DELAUNAY
ANALYSES", and "A MAZE-LIKE PATTERN IN THE MONODISPERSIVE LATEX SYSTEM".
My own subject is to construct the science on the indescribable
orders. In this paper, these materials
are rearranged together with other miscellanea so that my underlying philosophy
may reveal itself.
1. Introduction "A snowflake is a letter to us from the sky." "A diamond is a letter from the depth." These poems are by NAKAYA [1] and FRANK [2] respectively. The shape of a snowflake contains much information on the upper atmospheric conditions which have been experienced during its crystal growth. Similarly, the external form, the surface structure, the internal defects, etc. of a diamond contains much information on the states of the inside of the earth. Are we intelligent enough to decode the Ozma signals from nature fully? There are still many Rosetta stones waiting for Champollion to decipher the hieroglyphs on them (TERADA [3]). Among all kinds of orders in nature, our science could take subjects only on the easily quantifiable ones. As for the hardly quantifiable orders, even telling a Rosetta stone from others is difficult, much more deciphering the basic laws hidden in the hieroglyphs. We do not have enough concepts to set such indescribable orders on science. Wanted: more concepts, more approaches, more procedures, more methodologies, etc. In this paper, two attempts along this line are described. One is concerned with a digital description of the points distributed in a continuum space. Two opposite cases, the crystalline-like regular orders and the complete disorder without any correlation, are rather easily idealized and formulated as a scientific description. The correlations in the intermediate cases, as in the configurations of liquids and/or 'amorphouses'*), are indescribable without introducing some proper concepts. The digital description by the Voronoi-Delaunay scheme is promising for such cases. In order to firm the base of this scheme, the systematics of polyhedra and networks is necessary. The other attempt is concerned with a maze-like pattern in which a kind of frustration plays an essential role. There is a powerful description method for some problems in which all the possible local configurations are exhausted to construct the whole system consistently. It is the basic idea of KIKUCHI's cluster variation method [4]. The study of the maze-like pattern suggests a simple model which may possibly distinguish an amorphous state from a liquid state. The concept of percolation will be important. The
first attempt is described in Sec. 2. The second one is mainly given in
Sec.
3. In the last section miscellaneous discussions are also given including
the problem of the cultural background in science.
2. What can be seen from the Voronoi-Delaunay Analyses?
For a given configuration of atoms in a continuum bulk space, the VORONOI tessellation [5] and the DELAUNAY network [6], which are dual with each other, are uniquely carried out, affording a digital description [7]. Their definitions. which are depicted in Fig.1, are as follows. Definition of a Voronoi tessellation Suppose a configuration of N atoms in the space is given. Assign all the points in the space to their nearest atom, then the whole space is divided into N convex polyhedra. The mosaic structure obtained is the Voronoi tessellation for the given configuration. Each polyhedron, containing an atom inside, is the Voronoi polyhedron of the atom. Definition of a Delaunay network Join two atoms by a segment if their Voronoi polyhedra share a face in common. The obtained network is the Delaunay network. It is a tetrahedral tessellation if there is no degeneracy at all. The case in which five or more atoms happen to be on a sphere is called a degenerate case. 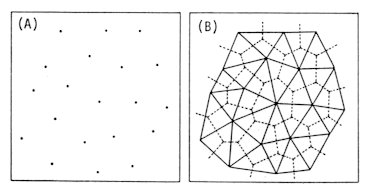
Fig.
1. Two-dimensional case (A). An atomic configuration
(B).
The most significant role which has ever been played by these concepts is that the crystallization could be concluded in a molecular dynamics simulation on the supercooled fluids of the soft core model [8,9,10]. The local crystalline order can be defined as the part where the Voronoi polyhedra are those which are characteristic of the crystalline order from the topological point of view. A crystallized part is distinguished from other part by this local definition. As for the disordered states, the decode of the hieroglyphs seems to be unsatisfactory. Some more information must be hidden in the Voronoi tessellation and/or the Delaunay network. The general scheme of the Voronoi-Delaunay analyses has not been fully established yet. Some confusion seems to exist in the current usage of the related similar concepts. It is desirable to make an effort to develop the hidden possibility of such remarkable concepts by clarifying the relationship between the similar problems. The aim of this section is to place the Voronoi-Delaunay analyses on a more solid foundation. A polyhedron, not necessarily a Voronoi polyhedron but in general, is usually classified as follows. First by the total number F of its faces as tetrahedron, pentahedron, hexahedron, etc. Secondly in more detail by the set {Fk} of numbers of its k-sided faces. Euler's relation V - E + F = 2 (1) is the most fundamental law concerned with the topological nature of polyhedra, where V is the number of vertices and E that of edges. A simple polyhedron is a polyhedron in which each vertex is shared by three edges and three faces. For a simple polyhedron, the relation 3V = 2E (2) holds and one of three numbers V, E and F determines other two. The corresponding relation for Fk's of a simple polyhedron is Sk=1µ (6 - k)Fk = 12 (3)
2.2. Finney's Scheme of the Voronoi Analyses Following
FINNEY [11], people conventionally use the distributions
and the average numbers of F and Fk in the Voronoi
analyses. The distribution of Fk contains more detailed
information on the topological nature of the concerned atomic configuration
of the whole system. This distribution is conventionally represented as
a histogram. However, the interrelation among {Fk}'s
is too complicated. They cannot be arranged in a one-dimensional way. In
order to derive hidden information contained in the distribution of {Fk}'s,
it is desirable to make the topological relationship among all the simple
polyhedra clearer. An attempt of systematics concerning the Voronoi-Delaunay
analyses is proposed in the succeeding subsections
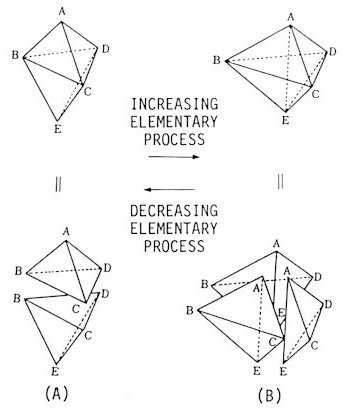
2.3. Elementary Process [12] Consider how a Voronoi tessellation changes into another when some displaced. Generally speaking, a Voronoi tessellation is stable in that it does not change by infinitesimal displacements. It is this that affords a digital description for the configuration in a space. The only exception to this stability is the degenerate case mentioned in the definition of a Delaunay network in 2.1. Such a case is very rare except in some regular configurations and does not affect the statistics of the Voronoi tessellation so long as its frequency is not proportional to the system size. Then people have hardly noticed an important positive role of the degeneracy in the theory of the Voronoi-Delaunay analyses. On the contrary, some people do not like the Voronoi-Delaunay analyses because the degeneracy takes place systematically all over an fcc lattice and an sc lattice. Note that a Voronoi tessellation changes into another only through an instantaneous degenerate configuration. Therefore we should investigate the details of such an elementary process that passes through a degenerate configuration. Suppose five atoms A, B, C, D and E are on a sphere in a moment. This is a typical degenerate case. Assume that atom E was outside the circumsphere of the tetrahedron ABCD and atom A outside that of BCDE before the moment. It means that two tetrahedra ABCD and BCDE were Delaunay tetrahedra sharing a triangular face BCD in common. as shown in Fig. 2A before the moment of degeneracy. If these atoms move smoothly during a small time interval containing the moment of degeneracy, atoms A and E are contiguous with each other as shown in Fig. 2B imediately after that moment. Note that there are three Delaunay tetrahedra ABCE, ACDE and ADBE now instead of two Delaunay tetrahedra ABCD and BCDE. Through this process, the number of Delaunay tetrahedra and equivalently the number of vertices of the Voronoi tessellation increases by just one.
Fig.2.
An elementary process process in the Delaunay aspect.
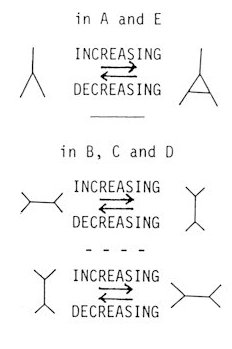
This change is reflected on the Voronoi tessellation in the way shown in Fig. 3. In each of two Voronoi polyhedra A and E, a vertex is cut off yielding a new triangular face. Three other Voronoi polyhedra B, C and D get changed topologically, but the number of the faces is conserved in each polyhedron. Therefore, this type of elementary process, in which five atoms participate, increases the total number of the faces of the Voronoi polyhedra in the whole system by two. Such a process may be referred to as an increasing elementary process. In a reverse process, the number of Delaunay tetrahedra decreases by one and the total number of faces of the Voronoi polyhedra in the whole system by two. The elementary process of this type may be referred to as a decreasing elementary process. A
process in which more than five atoms participate can be regarded as a
combination of these elementary processes. The possible numbers of Delaunay
tetrahedra which concern six atoms in the above sense are four and five
only.
A theorem, a corollary and two conjectures are proposed in this subsection. THEOREM: Some triangular faces are necessary to exist in order for a decreasing elementary process to take place. THEOREM directly follows from the definition of the decreasing elementary process given in the last subsection. If one regards THEOREM only as the problem of a polyhedral tessellation, the characteristics of the Voronoi tessellation are difficult to find. Note that a set of atomic positions is unique for a Voronoi tessellation. Thus the duality with the Delaunay network is the significant feature of the Voronoi tessellation in the polyhedral tessellation in general. The nature of the duality is not only topological but rather absolute in the sense that the absolute positions make sense. It is noted that the tessellation itself is absolute and a topological point of view enters only when it is analyzed.
Fig.4.
Stereoscopic figure of a KELVIN's tetrakaidecahedron (0608) in his original
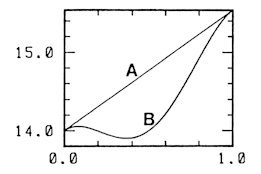
All the Voronoi polyhedra are KELVIN's tetrakaidecahedron [13], which is shown in Fig. 4, in the bcc configuration with only small displacements. This polyhedron with the index (0608) has no triangular faces among the fourteen faces. In the present point of view, the sc and fcc configurations belong to the same category as the bcc configuration [7]. One should count schematically as 6(1,0,0) + 8(1,1,1),= 14 for sc, (4) 12(1,1,0) + 1/3 × 6(2,0,0) = 14 for fcc. (5) Hereafter, the average number of the faces of a Voronoi polyhedron over a configuration is denoted by F. The following COROLLARY is easily derived. COROLLARY: The value F=14 for the bcc configuration in the above-mentioned generalized sense is the minimum value at least in the sense of local minimum. On the other hand, MEIJERING [14] proved rigorously F = (48/35)p2 + 2 = 15.54 (6) for the ideal gas configuration. These facts naturally suggest the following two CONJECTURES. CONJECTURE 1: In no atomic configurations is F less than 14. CONJECTURE 2: The value of F changes monotonically between the crystalline value and the ideal gas value along the physically meaningful path in the phase space. CONJECTURE 2 indicates also that 15.54 < F < 20 for the case of a diamond lattice, which corresponds to F = 20 as pointed out by SMITH [15]. In the case of F, one must obey the following two RULEs. RULE 1: All degeneracies must be removed. RULE 2: All the faces must be counted however small the area is. Otherwise the discussion given above cannot be applied. One may think RULE 2 is less meaningful. It depends on one's purpose. Some modified definition will be better for some purpose. What is important here is whether a general law can be seen or not under some proper definition. Unfortunately I can not prove these CONJECTURES. But rather firmly I am convinced that they are right. CONJECTURE 2 is very desirable in order that F is a meaningful quantity. See Fig. 5. If CONJECTURE 2 is wrong and the curve B in Fig. 5 is the case, a value slightly larger than 14 is taken by at least three different physically meaningful configurations. Similarly, a value slightly smaller than 14 is taken at least twice. Therefore, if CONJECTURE 2 is wrong, this quantity is a less interesting quantity since the agreement of this quantity never guarantees the closeness of the feature of the configuration.
Fig.
5. The value of F along a physically
meaningful path in the phase space under
One may think there are many counterexamples reported [16,17]. I dare to write NO. The present subject is that it should be noted that there are various other problems which are very similar to the present one, the Voronoi tessellation of a bulk space into simple polyhedra. Two RULEs mentioned above are necessary. For a finite system, the present theory is applicable only when the system is closed as in the case of some periodic boundary condition [10]. The important thing concerning this condition is closely connected with the discussion on the minimum size of the balanced region in subsection 4.1. In the problems of peas [18], bubbles [19], cells [20], shot-lead [21], grains [22], etc, faces are not always flat but curved. When curved surfaces are allowed, the situation is completely different. Then a biangular face can exist, a pair of faces can have many separated boundaries and even monohedron, which is topologically the same as a sphere, can exist. These are not allowed in a tessellation of an infinite space into convex polyhedra. If the restriction of the Voronoi tessellation is ignored, an example of less than 14 is easily constructed. Suppose here is a regular sc configuration. This is a degenerate case. The corresponding Voronoi cell is a cube. If a small regular octahedron is placed at each body centred point and correspondingly every vertex of the cubes is chopped off then the cubes change into (800006) tetrakaidecahedra. There are finaly the same number of two kinds of polyhedra, octahedra and tetrakaidecahedra. Then the value of F is (8+14)/2=11. It is noted that this polyhedral tessellation is not a Voronoi tessellation. The Voronoi tessellation of a CsCl-type configuration is the same as that of the bcc configuration. In two-dimensional case, the condition of the Voronoi tessellation brings nothing to the present problem. A corresponding two-dimensional elementary process conserves the number of Delaunay cells and then the number of edges too. This fact is closely connected with the fact that the three interior angles of a triangle add up to two right angles. Therefore a local fluctuation is always compensated in some other place in an infinite system. In three dimensions there are no such theorems. The regular polyhedra are only five Platonic solids: tetrahedron, cube, octahedron, dodecahedron and icosahedron. The last two of them, with five-fold symmetry, cannot take part in a crystalline order, though they are the members of five honourable figures of the highest symmetry [24]. A local fluctuation is not always just compensated and some overcompensation may be inevitable. The geometrical properties of two-dimensional space and that of three-dimensional space are thus different. The condition of a Voronoi tessellation certainly brings something in a three-dimensional case. This condition, though difficult to rephrase, is rather strong.
Fig.6.
Five Platonic solids shown in KEPLER's Harmonice Mundi [23]
octahedron, tetrahedron,
The
coordinates of the counterexamples to CONJECTUREs are welcome. They should
bring much information to correct my possible mistakes in the present attempt
of the systematics if any. They would also be able to characterize from
another point of view.
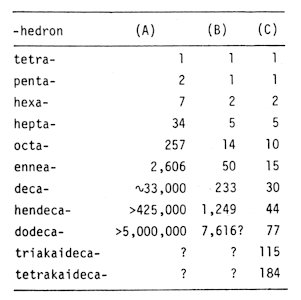
Topologically speaking, there is only one tetrahedron. The number of pentahedra is two, one is simple and the other is nonsimple. The number of the topologically different polyhedra has been studied in the field of discrete mathematics [25,26,27]. Some results are shown in Table 1. There are too many kinds of polyhedra to understand the relationship among them.
Table
1. The number of species of the polyhedra:
(A) total, (B) the simple polyhedra, (C) Fk= 0 for k>7.
It is possible, however, to define the degree of relationship among them through the elementary processes introduced in 2.3. See Fig. 3. The number of faces increases by the birth of a triangular face at a vertex accompanying some modification in the three related faces. Similarly, it decreases by the death of a triangular face. A change in the connectivity as in B, C and D shown in Fig. 3 may yield a new polyhedron. Anyway, all the polyhedra are connected only through some combination of these three processes. As a principle, the family tree of simple polyhedra can be constructed. See Fig. 7. Actually, it is a network rather than a tree. The degree of relationship between two polyhedra can be defined by the minimum number of the steps necessary to reach from one to the other on this family tree. It is very difficult to carry out the construction of a family tree up to round tetrakaidecahedra, which is the most important in the present discussion. See how vast the number of their species in Table 1. It is more practical to investigate first the relationship between some significant polyhedra. The polyhedron associated with the regular fcc lattice is the (0,12) rhombohedraldodecahedron if the degeneracies are left unremoved. It requires six half processes to the Kelvin's tetrakaidecahedron associated with the bcc configuration and also to the (0,0,12) regular dodecahedron associated with the so-called icosahedral configuration. Here the concept of half-process is introduced to express the elementary process starting with a nonsimple polyhedron. The
degree of relationship is easily generalized to between the Voronoi tessellations
and between the Delaunay networks.
2.6. Summary of the Section In order to get more information from a Voronoi tessellation and/or Delaunay network, an attempt to construct the systematics of polyhedra and tessellations was made in this section. In 2.3, two elementary processes, increasing and decreasing, are defined without passing through either of which a Voronoi tessellation cannot change into another. They are the base of the systematics. A THEOREM, a COROLLARY and two CONJECTUREs are proposed in 2.4. The family tree of polyhedra and the degree of relationship between polyhedra and between tessellation are introduced in 2.5.
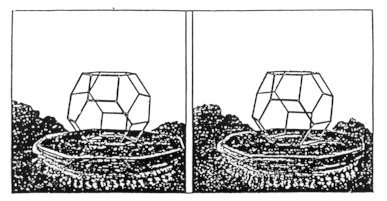
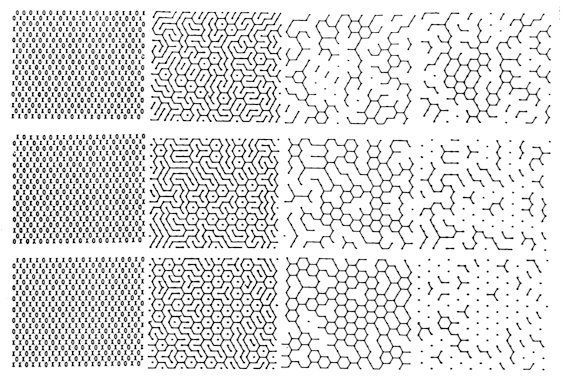
3.1. Some Experimental Facts A maze-like pattern has been observed in a monodispersive latex system in a thin gap between two glass plates by KOSHIKIYA and HACHISU [29]. The diameter of latex particles is about 7000A. The electrolyte used is 10-5mol/l KCl. The pattern is static in some cases and is moving in the other cases. In a sufficiently thin gap (~2), the latex particles form a two-dimensional triangular lattice in a layer. In a properly thick gap, their arrangement is uneven in a layer and the pattern appears. Here the texture of the bright looking particles and the dark looking particles construct the maze-like pattern. In Fig. 8A, of soft feeling, the sizes of the bright ones and the dark ones look similar on picture. In Fig. 8B, of hard feeling, the apparent sizes of the dark ones are smaller than that of the bright ones on picture. They are thinner and thicker cases respectively. In a too thick gap (~3), they form two layers without pattern. Each particle seems to lie in either of two states, upper or lower, at its lattice site. The details of the cases of thicker gaps are described in 3.4. Two neighbouring particles prefer different states with each other so that they have bigger free volumes. Then the system is analogous to the antiferromagnetic Ising model of a triangular lattice, which is a typical frustrated system. The ground state of this model is degenerated and the residual entropy at absolute zero is rigorously estimated by WANNIER [30].
Fig.
8. A latex system in a narrow gap shows a
maze-like pattern (pictures through
Let us take an antiferromagnetic Ising model on a triangular lattice. Suppose the number of lattice sites is L and then that of nearest-neighbour pairs is 3L. A basic cell is defined as a regular triangle consisting of three sites which are nearest neighbour with one another. The number of such basic cells is 2L. Let us confine our consideration to a set of configurations which belong to the degenerated ground states. It may be referred to as the ground state ensemble. In any member of this ensemble, as easily seen, three sites in a basic cell never are in the same state; two of three sites are in one state and the other site in the other state. This constraint, which is hereafter referred to as the basic constraint, characterizes the ensemble.
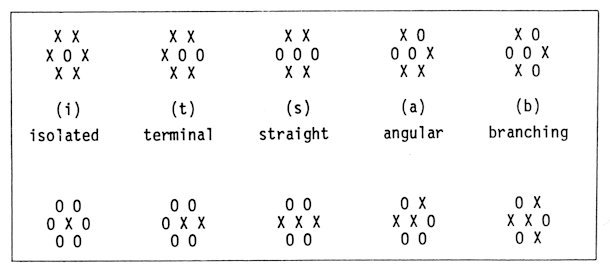
A cluster is defined as a set of the sites in the same state which are connected by the nearest-neighbour bonds. As for a site in one state, the configuration of its six neighbours is restricted to either of the five types shown in Fig. 9. The classification is based on the part of the central site in a cluster. It directly follows that any cluster does not have width and that the pattern of the whole system is maze-like in most cases. It sometimes takes place that a cluster of one state is a network like a honeycomb lattice and that of the other state is isolated, distributing as in a triangular lattice with a larger lattice constant. Some simulated configurations are shown in Fig. 10.
The probability of five types of configurations in the ground state ensemble are calculated by making use of the KIKUCHI's cluster variation method [4], which is the systematic generalization of the Bethe approximation. A hexagon consisting of seven sites, one at the centre and six at the corners as in Fig. 9, is chosen as the basic figure. The number of allowed configurations on it is ten, twice of the above-mentioned five in view of two possibilities at the centre. If the equivalence of two states, 0 and X, is assumed, the number of configurations is essentially five. Then the number of independent variables is finally reduced to two. The basic equation of the cluster variation is easily solved and the probability of five configurations in Fig. 9 is given as follows, (i) 0.0168, (t) 0.0180, (s) 0.0194, (a) 0.0292 and (b) 0.07099 where the symmetry factors by the existence of the equivalent configurations in various directions are not taken into account. If they are included so that five numbers add up to 1, the probabilities are rewritten as (i) 0.0336, (t) 0.2165, (s) 0.1163, (a) 0.3500 and (b) 0.2836. The
entropy in this approximation is 0.3154 and is satisfactory. It should
be compared with the rigorous value 0.3231 obtained by WANNIER [30]
and corrected by DOMB [31].
3.3. The Comparison Between the Simple Model and the Latex System Though
the comparison of the theory with the latex system is now only preliminary
and qualitative, the following may be pointed out.
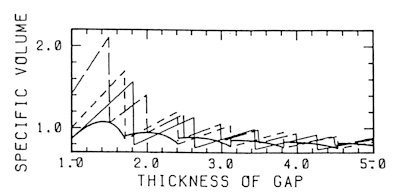
Let us consider the regular packing of hard spheres in a narrow gap in order to give a base to the simple model and to explain why the straight part appears rather much. An elementary calculation leads to the result shown in Fig. 11. The packing scheme of the closest arrangement changes kaleidoscopically with the thickness of the gap. Most of them can be regarded as a sliced piece of an fcc crystal in some direction. A stripe type structure is continuously deformable, including these sliced lattices as the special limiting cases. The packing of this type is very efficient in a thin gap.
Fig.11.
Packing efficiency in a gap in various schemes: the saw-toothed lines,
--- stands
If
the irregular packings are included, the situation in the limit of monolayer
is modified because of the entropy of the degenerated disorder packing.
The just limit is expected to be very close to the ideal nearest neighbour
model. By the combination of these arguments, the tendency for the straight
pattern is essentially interpreted. It is also interpreted why a pattern
in a thinner gap gives a soft feeling and those in a thicker a hard feeling.
In a thinner case, the apparent sizes of bright one and dark one are almost
the same. Their arrangement can be approximated as a triangular lattice.
The difference is only in brightness. In a thicker case, the dark ones
lay behind the bright ones and the tendency to the stripe structure is
stronger.
3.5. Maze-Like Patterns in Nature The origin of the maze-like pattern in the latex system was interpreted in this section. It is one of the mechanisms yielding a maze-like pattern. It is interesting that very similar maze-like patterns are found rather widely in nature. For example, in the magnetic domains of garnets and in the marking of some fish [32], in the brain coral [33] and in the magnetic liquids [34], etc. See Fig. 12.
Fig.12.Signus javus, magnetic domains and a brain coral [32,33]. These
are the continuous systems and the mechanism of yielding a meandering maze-like
pattern is not completely the same as that in the latex system. But the
present method of analysing patterns will be applicable to them in some
stage. It is also applicable to the volume exclusion problem of polymers.
Some of five configurations in Fig. 9, (i) and (b)
for example, are forbidden in such a case. To go beyond, however, it is
desirable to extend Kikuchi's view to continuum.
4. Miscellaneous Remarks
Though an amorphous material is homogeneous or uniform as a bulk system, it is not so in a small scale. Various models have been proposed as the local characteristic to amorphouses. None of them can be extended infinitely. Some other structures are, necessary in order to fill the whole space. As a model of a bulk amorphous, one should take the balance of these two structures or more into account. Otherwise, the model of amorphous structure will be as confused as the case of the seven blind men and an elephant. There must be a critical value of the system size smaller than which the system can not be regarded as effectively homogeneous. Of course this size depends on the details of the system. However, the minimum size in a narrow sense should exist which is independent of the details of the system and is determined by the geometrical property of the space. This size is also required to perform a computer simulation in order to get some information of a bulk amorphous. In a simulation of a liquid state, various types of configurations appear in a time sequence. But, it cannot be expected in that of an amorphous. It is the very feature of an amorphous. The coexistence of two local structures should not be expected as appearing chronologically but spatially in an amorphous. Now,
only very rough estimation of this size can be done. In a Lennard-Jones
system, the icosahedrally grown microcluster is energetically preferable
to that with fcc-like structure in the system size range of less
than some hundreds atoms [35]. To have a balanced
coexistence of two types of region, the minimum size required cannot be
less than a thousand. Perhaps 103 or 104 will be
a conservative estimation. But the size of an elephant is clearly too radical.
If CONJECTURE 1 in subsection 2.4 is right, the system
whose Voronoi tessellation corresponds to the F value of less than
14 is too small to be regarded as a bulk system.
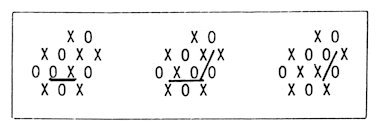
4.2. A Possible Distinction Between the Liquid and the Amorphous Apart from the latex system, the antiferromagnetic Ising model on a triangular lattice, which is studied in Sec. 3, is very interesting. It may give a qualitative or conceptual model to distinguish a liquid from an amorphous. Sometimes a lattice gas model is used to derive three phases (gas, liquid and solid) by a single simple model for the purpose of qualitative understanding of the essential point. It is desirable to include the amorphous state in such a model. To avoid unnecessary difficulty, however, we may focus on the distinction between a liquid and an amorphous, discarding the two other phases. Regard the system as a lattice gas model on a triangular lattice. If the number density is kept constant, the feature of the configuration depends on the constant value of density. See Fig. 10. The configuration at high density looks like the well-known Zachariasen structure, in which the network part percolates. For smaller densities, the network part is localized. There would be a critical density of the percolation in this sense. However, the distinction between liquid and amorphous should be more kinematic. The following kinematical law of motion is introduced. The states in a nearest-neighbour pair can be exchanged if they do not violate the basic constraint mentioned in 3.2. This mechanism conserves the number of sites in each state and may be suitable as a lattice gas model of dmorphous. It takes place only when two neighbouring sites are in one state in the configuration (a) and in the other state in the configuration (b). See Fig. 13. Two sites in an underlined pair can exchange their states without violating the basic constraint. After two sites exchanqe their states, some immobile parts in the neighbour become mobile as shown in this figure.
Fig. 13. The underlined pairs can exchange their states. It is noted that the mobility depends on the density. Sometimes a mobile part propagates to the infinite distances in the above-mentioned mechanism. In some other cases, a mobile part itself does not, but the correlations of some mobile parts make the propagation to an infinite distance possible. Anyway, some kind of concept of percolation will be proper to define a liquid from this point of view [36]. In other cases, the mechanism of motion does not make a path from a configuration to another. Then the configurations of the whole system are divided into many families: the configurations in the same family are connected by the allowed mechanism and those belonging to different families are disconnected. An amorphous state may correspond to such a situation. Such
a kinetic lattice gas model will be the simplest to lead the distinction
between a liquid and an amorphous. The present model has a kind of scaling
property. The model is specified by only two independent parameters. One
is the mobility parameter which is related with temperature. The other
is the density. Then the glass transition, if it exists in the model appears
as a critical density.
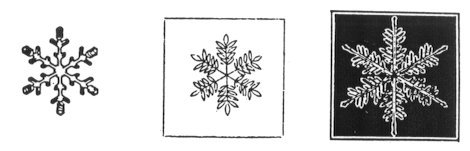
4.3. Science of Shapes, Forms and Patterns In the present symposium, various types of shapes, forms and patterns in nature appear in many papers. I was strongly impressed that a kind of nucleation process is certainly going on at many places all over the world. Nucleation of organizing scientific ideas and attempts in various individual branches of science to construct the science of indescribable order. Two domestic meetings based an such a point of view were already organized in Japan since 1980 as the project of the Research institute for Fundamental Physics, Kyoto University [37]. The participants include physicists, mathematicians, statisticians, biologists, biophysicists, topographers, architects, city planners, anthropogeographers, dendrologists. etc. The third one will be held in February, 1983, supported by Grant-in-Aid for Scientific Research from the Ministry of Education, Science and Culture. A similar plan is in progress in England by Weaire and Rivier. The problem is how to construct the science on the indescribable order which people can surely recognize through all their senses, but which is hardly quantified to give a formulation as an exact science. The demand for concepts of decoding the hieroglyphs is surely increasing. For example, the pictures from a weather satellite must contain enormously massive information, not only a huge assembly of microscopic information but also indescribable global pattern information. Without introducing proper concepts, we can not construct science of such a 'new Nature'. Some pioneering works by Japanese scientists in the field of decoding patterns seems to be unknown to the western scientists. On this occasion, I like to mention some of them briefly. In 1833, DOI (1789-1848) published a book showing his sketches of various types of snowflakes, which are based on his observation through a 'Dutch Glass' (microscope) [38]. His sketches are fully objective. Comparing them with those by western people, Kepler, Descartes, Hooke, Rossetti, SCORESBY [39], GLAISHER [40], etc., KOBAYASHI noticed some similarity lies between some of Doi's sketches and some of Japanese family crests [41]. He pointed out the pattern recognition depends on one's cultural background.
Fig.
14. Sketches of snow crystals through a microscope
from nearly the same period:
TERADA (1878-1935), who interpreted the Laue spots independently of Bragg in the same year 1913, made many pioneering works on various topics on patterns together with his collaborators [42]. His theme covers cracks, fissures, sparks, vortices, various phenomena similar to Liesegang rings, etc., especially from a morphological point of view. What are now called operations research and simulation are also covered. NAKAYA (1900-1962) [1] was a student of his. HIRATA (1906-66) proposed an analogy between the origin of the marking of the giraffe and that of the cracks at the surface of a gradually drying mud pool [43]. Some biologists opposed such an inorganic point of view. Studying the physical morphology of colour pattern of some domestic animals, Terada supported Hirata's bold and flexible idea. Now, a similar analogy is seen in the book by STEVENS [33]. Later, Hirata developed the stochastic theory of fracture.
Fig.15. The marking of giraffe and mud cracks.
4.4. In an Aspect of Comparative Culture Japanese gardens are geometrically less ordered than Western gardens. They are less symmetrical and the fundamental law regulating their geometrical structure is difficult to express concisely. Nobody, however, regards them as chaotic. When Lee visited a Japanese garden together with Yukawa, he said that its entropy is very low and agreed to MATSUDA's words "like that of a biological object" [44]. The underlying aesthetic sense of constructing a Japanese garden is 'harmony'. 'Harmony' can be regarded as a more inclusive concept than 'order'. No later than eighth century, some Greek design and Arabesque are introduced through the Silk Road. Original Arabesque is more crystalline like and the Japanese designs affected by them are more irregular, aperiodic or, so to speak, more amorphous-like. See Fig. 16. (The correspondence is not in an exact sense). Japan locates at the end of this propagation route. If one goes beyond, the Pacific ocean lies there. The design will melt into water.
Fig.16.
A typical Arabesque design and the back of a Japanese bronze
What
enabled such harmonized irregularity is some artistic sense and/or feeling
of harmony or balance. The cultural background of Japan may be very suitable
for the construction of science on the amorphous structure or more generally
on such indescribable order or harmony. Of course, science is universal
and international. But, the facility of recognizing a certain fact sometimes
depends on one's cultural background, especially in some unestablished
fields where some new concepts are desired.
Acknowledgements I
would like to thank Dr. M. Tanemura and Dr. N. Ogita for useful discussions
on the Voronoi-Delaunay analyses, Prof. S. Hachisu and Mr. Y. Koshikiya
for the information on their experimental results on the latex system before
publication. I also thank Prof. T. Kobayashi, Prof. K. Higuchi and Mr.
K. Omori for the information on the literature on T. Terada and U. Nakaya.
I am indebted to Dr. 0. Ishii for the arrangement of the picture on the
magnetic domains in a garnet and on Siganus javus. Subsection 4.4 is partly
based on the conversation with Prof. J. F. Sadoc, Prof. K. Kawamural. Prof.
T. Fujiwara, Prof. K. Kitahara, Dr. S. Miyashita, Dr. H. Takano and Dr.
H. Kawamura during a short Kyoto tour after the symposium.
References: [1] U. Nakaya: Snow Crystals: Natural and Artificial, Harvard Univ. Press, 1954. The poem appears in U. Nakaya: ' Yuki (Snow)' (A monograph written in Japanese), Iwanami, 1937. [2] F.C. Frank: Science and Technology of Industrial Diamond, 2, 119 (1967). [3] In Nakaya's monograph [1], the poem follows immediately after the quotation of the Terada's metaphor of volcanic ejecta by Rosetta stone in T. Terada: 'Ko-Asama (name of a volcano)', (An Essay in Japanese). [4] R. Kikuchi: Phys. Rev. 81, 988 (1951). [5] G.F. Voronoi: J. Reine Angew. Math. 134, 198 (1908). [6] B.N. Delaunay (Delone): Bull. Acad. des Sci. USSR, Classe Sci. Math. Nat. 6, 793 (1934) Soviet Math. 2, 812 (1961). [7] T. Ogawa and M. Tanemura: Prog. Theor. Phys. 51, 399 (1974). [8] The crystallization into bcc-like order was first reported in M. Tanemura, Y. Hiwatari, H. Matsuda, T. Ogawa, N. Ogita and A. Ueda: Prog. Theor. Phys. 58, 1079 (1977). There, the Voronoi tessellation is made for the 'averaged' configuration over a certain time interval not for the instantaneous one to see the order more clearly. [9] The crystallization into an fcc crystal is analyzed in M. Tanemura, Y. Hiwatari, H. Matsuda, T. Ogawa, N. Ogita and A. Ueda: Prog. Theor. Phys. 59, 323 (1978). The technique of a uniaxial deformation is adopted to see an fcc order as a bcc-like order. [10] Our computer algorithm of the Voronoi tessellation is to be published in M.Tanemura, T.Ogawa and N.Ogita: J. Computational Phys. [11] J.L. Finney: Proc. Roy. Soc. A319, 479, 495 (1970). [12] T. Ogawa: 'Suri-Kagaku (Mathematical Science)' (in Japanese) No.231, 7 (1982). [13] W. Thomson (Lord Kelvin): Proc. Roy. Soc. 55, 1 (1894). [14] J.L. Meijering: Philips Res. Rep. 8, 270 (1953). [15] F.W. Smith: Can. J. Phys. 43, 2052 (1965). [16] J.A. Barker, M. R. Hoare and J. L. Finney: Nature 257, 120 (1975). [17] R. Yamamoto, H. Shibuta, T. Mihara, K. Haga and M. Doyama: Proc. 4th Int. Conf. on Rapidly Quenched Metals, ed. by T. Masumoto and K. Suzuki, (Japan Inst. of Metals, 1982), Vol. 1, p. 283. [18] S. Hales: Veqetable Staticks, Innys and Woodward, London, 1727. [19] D'Arcy Thompson: On Growth and Form, Cambridge, First ed. 1917, Second ed. 1942. [19a] E.B. Matzke: Amer. J. Botany 33, 58 (1946). [20] J.W. Marvin: Amer. J. Botany 26, 487 (1939). [21] J.W. Marvin: Amer. J. Botany 26, 280, 487 (1939). [21a] E.B. Matzke: Amer. J. Botany 26, 288 (1939). [22] C.H. Desch: J. Inst. Metals 22, 241 (1919). [23] J. Kepler: Harmonis Mundi, (1619). Kepler is supposed to be the first who studied the problem of covering a plane by congruent regular polygons and noticed that five- and seven-fold symmetry contradict the crystalline order. [24] T. Ogawa: Z. Phys. B28, 73 (1977). Especially, see Sec. 1 of this paper. The difference between two and three dimensions was also discussed in Sec. 5 of Ref. [7]. [25] B. Grünbaum: Convex Polytopes, Interscience, 1967. [26] P.J. Federico: J. Combinatorial Theory 7, 155 (1969). [27] M. Hucher et J. Grolier: Comptes Rendus 284, A220 (1977). [28] A preliminary report is to be published in T. Ogawa: J. Phy. Soc. Japan. 52 (Suppl.) (1983). [29] Y. Koshikiya and S. Hachisu: Lecture at COLLOID SYMPOSIUM of JAPAN (1982). [30] G.H. Wannier: Phys. Rev. 79, 357 (1950). [31] C. Domb: Adv. in Phys. 9,149 (1960). [32] The similarity between the pattern of the magnetic domains and that in the marking of Siganus javus is noticed by E. Feldtkeller and O. Ishii. Feldtkeller: private communication through O. Ishii. O. Ishii: Electronics Journal (in Japanese) 17, 1716 (1972). [33] The similarity between the pattern of the magnetic domains and that in the brain coral is pointed out as the meanders in P.S. Stevens: Patterns in Nature, Little, Brown & Co., 1974. [34] R.E. Rosenweig: Scientific American, 247, No.4, 124 (1982). [35] M.R Hoare: Adv. in Chem. Phys. ed. by I. Prigogine, Vol. 40, p. 49, Interscience, 1979. [36] M.H. Cohen and C.S. Crest: Phys. Rev. B20, 1077 (1979). [37] The proceedings have been published in T. Ogawa (ed.): 'Bussei Kenkyu (mimeographed circular in Japanese)' 36, A1 (1981). The author's philosophy as an organizer is mentioned in T. Ogawa: 'Butsuri (Bulletin of Phys. Soc. of Japan)', (in Japanese), 36, 867 (1981). [38] T. Doi: 'Sekka-Zusetsu (Illustration of Snow Blossoms)', (in Japanese), (1833) and 'Zoku-Sekka-Zusetsu (continued)' (1840), reprinted with a commentary in Japanese by T. Kobayashi, Tsukiji Shokan Pub. Co., Tokyo, 1966. (Revised ed. 1981). [39] W. Scoresby: An Account of the Arctic Regions, with a History and Description of the Northern Whale-fishery, Edinburgh, 1820. [40] J. Glaisher: (1855), cited in G. Hellman: Schneekrystalle, Berlin, 1893. [41] T. Kobayashi: The commentary on Ref. [38], (1968). [42] T. Terada: Scientific Papers, vol. 1-6, Iwanami, 1937. Main literature on Terada written in English is as follows, P.P. Ewald (ed.): Fifty years of X-Ray Diffraction, Intn. Union of Crystallography, Utrecht, 1962; B. Tamamushi: Philosophical Studies of Japan, Japanese National Commission for UNESCO, Tokyo, Vol. 8, p. 117, 1967. [43] M. Hirata: 'Kagaku (Science, in Japanese)' 3, 461 (1933). M. Hirata: Sci. Pap. Inst. Phys. Chem. Res. 26, 122 (1935). (On the origin of coloured patches of some kidney-beans.) See also K. Henke: Zool. Anz. Supplbd. 8 (1935). [44] H. Matsuda: in Physics of Random Systems, (in Japanese), ed. by Phys. Soc. of Japan p.1, Bai-fu-kan, 1981.
*) In the following, I shall use the word 'amorphous' as a noun to mean anything amorphous: such as amorphous state, amorphous structure, etc. ERRATA and COMMENT added in March. 1984
CONJECTURE 1 in p.64 is wrong at least in the literal sense or purely geometrical sense.
In some regular alloy structures,
F is less than 14 as pointed out by Nelson (Phys. Rev. 28 (1983) 5515);
(12 + 3×14)/4 = 13.5, (2×12 + 16)/3 = 13.33 in Laves' phase and other
structures called Frank-Kasper phases.
In spite of these counter examples, I believe that It is worth to be
particular about the number 14, to characterize such configurations
in other words, especially as the problem of the one-species spherical particles. On the Science on Form added in July, 1985
In p. 73, some description is given on the interdisciplinary
research cooperation on Science on Form. In cooperation with
the Stereology group. Society for Science on Form, Japan was
founded in March of 1985 to organize domestic symposium several
times a year and some international symposium and to publish a Journal.
The first International Symposium for Science on Form is to be held at
Tsukuba in Japan in 26-30 November, 1985.
The original paper is published in Topological Disorder in Condensed Matter. Eds. F. Yonezawa and T. Ninomiya, (Springer Verlag, 1983) (Springer Series in Solid-State Sciences 46) p.60-77.
|