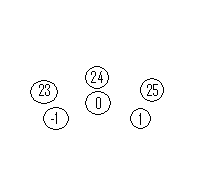I believe the universe is a great symphony of numerical correspondences,
I believe that numbers and their symbolisms provide a path to special knowledge. 

-Umberto Eco
 
 

There are many mysteries in our world, one of which is the tonal system. I have often heard theorists marvel at how there is something "so right about it." Indeed, the music of Bach and other masters of tonality remains one of the magical delights of our existence, in part because it inexplicably makes so much sense. There can be no doubt that the tonal system is one of our most ingenious discoveries. In some ways it may be better that the secrets of music remain something that we can not explain, however it seems that music is once again entering the picture as a model for understanding the nature of nature. A prime example is string theory, an important relatively new theory among physicists today that has a familiar ring to it (pun not intended). Given that there is a renewed interest in understanding string theory, there is good reason to investigate the nature of the tonal system as something from which we can learn secrets about our world. Hence, music is once again a science. Should it have ever been separated from its siblings in the quadrivium?
 
 

I have often wondered why there are seven scale degrees in the tonal system. My teachers told me about Pythagoras and the interesting nature of acoustics, but I never heard a satisfactory explanation as to why he (if he really was the inventor of the system) had decided to use the seven pitch names. I have heard the explanation that the Pythagoreans constructed the heptatonic scale from the notion among the Greeks that there were seven planets. The story was very mystifying and I remember wondering whether the discovery of the extra planets undermined the perfection of this system. If he were alive today, would Pythagoras hold a press conference and admit his great disappointment at having extra planets to account for in his model? My research leads me to believe that neither the extra planets, nor the misidentification of the moon and sun as two of them, would have bothered the wise one at all. However, if there is no planetary justification for the seven letter names, then how do we account for the system settings? 

The answer to this question is an interesting one that points to the importance of aspects of number theory in providing a basic model for understanding the structure of the tonal system. The particular aspects of number theory which I believe are the basic organizational principles of music seem to have broad applications for not only music, but for understanding important mathematical properties of numbers and their relationship to geometry, periodicity, symmetry, and proportion. I have attempted in this paper to put together some of the pieces of the puzzle of tonality. I have tried to avoid heavy mathematical discussion, confining it only to that which is necessary to understand the system that probably originated with the ideas of Pythagoras and the Pythagoreans, but which the Babylonians or Egyptians may have formulated well before the time of the Pythagoreans (ca. 500 BC). 

We know today that many of the notions put forth by the Pythagoreans concerning the structure of the cosmos are erroneous. The Pythagoreans attempted to explain the laws of nature with a basic model that they applied to many aspects of their experience of life, as I will discuss in detail below. The fact that the early Greek concept of the structure of the universe is flawed seems to have led to a complete dismissal of the possibility that the model they applied to the cosmos and to other phenomena such as the tonal system derived from some valid theoretical notions. My research suggests that there is a mathematically valid basis to the original model, by which the Pythagoreans described, among other aspects of the natural world, the tonal system. I hope to offer evidence that there are properties of whole numbers which, while at one time were part of the Pythagorean lexicon, seem to have been disassociated from the part of music theory, especially laws of proportion and string vibration, which survived and was transmitted to the medieval theorists such as Boethius. I will present what I think is a basic mathematical model by which tonal music, the phenomenon of acoustics, and other systems are unified. In conjunction with the mathematical properties that I discuss, I attempt to relate concepts of number theory to music theory because my ultimate goal is to provide the reader with an insight into the nature of what we experience when we hear music, and perhaps, a new way to analyze and interpret music. 
 
 

The discussion begins appropriately enough with Pythagoras who may have been one of the first string theorists. His study of the monochord supposedly led to the codification of much of what has come down to us as tonal theory. History has left us with no written documents authored by Pythagoras himself. Scholars have discovered that earlier civilizations such as the Chinese knew of the theorem for which he is most famous well before his time. In fact, we know very little about Pythagoras or of his true legacy. When we speak of the teachings of Pythagoras, we are generally referring a body of knowledge associated with those members of his school, known as Pythagoreans, who lived from about 550 B.C. to 350 B.C. Even investigating the mathematics of the Pythagoreans is a complex problem for scholars mainly because, as with Pythagoras, there exist no surviving original documents. Much of the information that we know regarding the Pythagoreans comes from second-hand sources written anywhere from 500 to 1000 years after Pythagoras and his followers were alive. It is probable that some of the theories, which connect the various surviving artifacts of the Pythagorean lexicon, were lost in antiquity. For example, some scholars such as Walter Buckert, an expert in the history of Greek philosophy, believe that the more mathematical and physical properties of acoustics and string theory are merely later additions to Pythagorean music theory. In Buckert’s opinion, the earliest Pythagorean concept of music was based more on "reverence for certain numbers and their role in music and cosmology" than on mathematics or experimental physics (Buckert, p.400). Again, it is very hard to tell how or when the Pythagoreans formulated their theories, and Buckert’s view seems to suggest that there was no one person such as Pythagoras himself who made the connection between the number theory and the acoustic theory that arises in the Pythagorean lexicon. I would like to suggest that there is good reason to believe that there was at one time a unified theory of music whose elegance implies a single creator. What follows are pieces of information that comprise some of the basic ideas from which Pythagoras may have constructed a model of the tonal system. 

Pythagoreans believed that there was an overall organizing principle associated with number. Their ideas suggest that numbers are not just abstract symbols invented by humans to count sheep; rather, they are the basic structural components of the physical world, a view similar to the more modern one of the atom as a basic unit of matter. Numbers had special properties that gave them specific character. For example, Pythagoreans associated odd numbers with masculinity and even numbers with femininity, so the first three numbers then represent the duality of gender. In Greek thinking the number one was both male and female, as it was the monad, a representation of God. Two then was the "mother" of number, therefore the first female number, and three was the first masculine number, so that all the subsequent even numbers were female and the odds were male (Hopper, p.39). 

Another important attribute of the Pythagoreans was that they directly connected numbers to geometry by organizing them into geometric patterns. According to mathematics historian Morris Kline, the Pythagoreans thought of numbers as "geometrical dots," usually depicted with pebbles in the sand. They categorized numbers according to geometrical shapes produced by their arrangement. There were square numbers, triangular numbers, oblong numbers, pentangular numbers, and more. For example, the numbers 1,3,6,10,15… (1, 1+2, 1+2+3, 1+2+3+4….etc.) are the triangular numbers because their arrangements produce equilateral triangles (see Figure 1). The numbers 4, 9, 16, and 25 are examples of square numbers because they produced a square shape when arranged geometrically.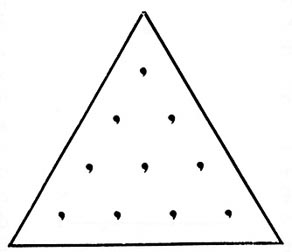

Figure 1: The Pythagorean Tetraktys.

In the Pythagorean concept of numbers, the number four contained the number ten because it was seen as a combination of itself and the numbers one, two, and three, that come before, producing the arrangement of an equilateral triangle. This type of thinking is a good example of the association of numbers to geometry mentioned above. Kline states that the number ten and its geometric representation was particularly special to Pythagoreans: "The fourth triangular number, 10, especially fascinated the Pythagoreans because it was a prized number for them, and had 4 dots on each side, 4 being another favorite number" (Kline, pp.29-30). Another scholar, Annemarie Schimmel, explains that the number ten in its geometrical form (1+2+3+4) held special significance because it "was associated with the primordial one existence (1), the polarity of manifestation (2), the threefold activity of the spirit (3), and the fourfold existence of matter as seen in the four elements:" air, fire, earth, and water (Schimmel, p.180). The tetraktys, shown above in Figure 1, is the basis of the model that was a keystone to Pythagorean theory. Below I list some of its more significant features. 

• The tetraktys represented the number 10 generated from the sum of the first four whole numbers:

• Another significant aspect of the tetraktys is that the numbers 1,2,3 and 4 form the numbers of the prime ratios that create the perfect intervals in the tonal system and serve as the basis for the construction of the Pythagorean heptatonic scale:

• One final interesting facet of the tetraktys is that the product of its four numbers is twenty-four, a fact that offers a link to the relationship of numbers to space and time that I will discuss later.

The geometrical aspect of numbers, as represented by the tetraktys, played an important role in Pythagorean thinking and seems to be the unifying element in how they understood the organization of many aspects of nature including the tonal system. Christopher Butler maintains that it was Pythagoras himself who "first stated the mathematical relationships involved in musical harmonic relationships" (Butler, p.4). Butler goes on to make the case that the Pythagoreans found great significance in the revelation of their founder.

The tetraktys then was the basis of the model with which the Pythagoreans attempted to explain the structure of the world in various ways. For example, in the Pythagorean conception of the universe there were precisely 10 celestial bodies, the Earth, the Sun, the Moon, five other known planets, plus one outer sphere representing the so-called fixed stars, and one other sphere, the counter-earth (more about this rather bizarre planet later). The number ten was also important because there were supposedly ten sets of four elements in the world that the tetraktys symbolized. In short, the tetraktys "was treated as a key to the understanding the whole of life" (Butler, p.9).

The Pythagorean model of the cosmos and the related notion of the Music of the Spheres, were macrocosmic applications of the phenomenon that Pythagoras or others before him had observed from the study of strings and other properties of numbers expressed by the tetraktys. Of course, the Pythagorean study of strings remains to this day an important basis for understanding the structure of the tonal system. The study of number proportions and its application to music was a source of fascination for theorists throughout the middle ages and into the renaissance. This aspect of Pythagorean theory survives today as an essential component of the modern study of acoustics and the physics of music. 

However, I believe that there is more to the mystery of the tonal system than what we find in the study of acoustics, as I will discuss below. I avoid much focus on the topic of proportions or string theory because, while important, I think it is an accepted part of music theory that needs little elaboration. Instead, I concentrate on what I believe is the lost component of the teachings of Pythagoras, a subject more involved with number theory than acoustics, but which, like string theory and acoustics, has important musical applications. 
 
 

The Greeks inherited the decimal system from the Egyptians who most likely established it. The number ten and the tetraktys had the special significance mentioned above, therefore it is plausible to consider that the underlying organization of the seven-pitch tonal system is based on the number ten as represented in the tetraktys. For the purposes of this discussion, I will refer to this hypothetical model of the tonal system as the tetraktys model. How does this model based on ten produce seven pitches for the tonal system? Answering this question is the key to understanding some aspects of the mystery of tonality. I believe as well that part of the answer reveals that, at the time of Pythagoras and well before, there was a way known of organizing numbers in cyclical and periodic systems which take into account the relationship of number to space. I also think that this system of organization reveals how numbers themselves and music operate according to symmetrical and periodic properties as a natural function. In effect, there are hidden principles of mathematics that create the organization of music which for some reason have been lost to antiquity until recently. In order to understand the organizational principles to which I am referring, it is necessary to study in more detail aspects of the number theory of the Pythagoreans.

Further investigation into Pythagorean and Greek thinking about numbers reveals that they did not really think of the numbers 1 and 2 as numbers at all. Interestingly, for them the numbers actually begin with three. Laurence P. Shrenk, a scholar of the history of Greek philosophy states "for the Greeks 'one' was not, in the strict sense, a number, but rather, the unit of numbers; it is the 'identification' out of which number is generated" (Schrenk, p.5). Schrenk suggests that the Greeks began the counting numbers with two, however other scholars such as Vincent Hopper and Sir Thomas Heath, suggest that three is the first number:

Now we can begin to see why seven pitches occur in the system; it may be because the first three numbers reduce to a sort of grouped complex. This possibility is an important link to how numbers occur in relation to spatial organization, which, it turns out, is an important aspect of the Greek concept of the structure of the universe. Heath notes that Pythagoras "was one of the first to maintain that the earth and the universe are spherical in form" (Heath, p.162). While Heath suggests that the reason Pythagoras came to this conclusion stems from the aesthetic beauty of the sphere, there is reason to think that Pythagoras’ conclusion relates more to the fact that the sphere is geometrically the most efficient arrangement of matter in three-dimensional space. The Pythagorean organization of the planets and the ancient "science " of astrology are macroscopic applications of a basic number theory in relation to geometry. In effect, the Greeks applied the tetraktys model to the macrocosmic level in attempting to hypothesize about a spherical the organization of the planetary system. 

In the Greek concept of the arrangement of the natural universe, the planets were spheres that revolved around the central fire in ten concentric circles (Heath, p163) ¹⁾ . However, as mentioned above, there were only seven observable heavenly bodies besides the earth, and the fixed stars arrayed in their own outer sphere. Scholars suggest that this is why an extra body, the counter-earth, was invented: The Pythagoreans needed this hypothetical planet which "always accompanies the earth" in a smaller orbit and could never be seen because it was always on the other side of the hemisphere away from which the Greeks lived (Heath, p.164). Aristotle ridiculed the idea of the counter-earth along with other aspects of Pythagorean thinking.

It is interesting that, with his skepticism, Aristotle overlooks the possibility that, although the notion of the counter-earth is unsupportable by observation, there may be some other reasons why the Pythagoreans invented it, not merely to fit their preconceived notions ²⁾. Just because a theory is wrongly applied, the basic concept behind the model may still be sound. There is evidence to suggest that there is a strong theoretical basis behind the tetraktys model. In reference to this, German scientist and author, Peter Plichta, presents some very cogent observations regarding the significance of this aspect of Pythagorean theory that I believe is an important basis of the tonal system. "Pythagoras realized that the vibrations in the full, half, third, and quarter string of the monochord" (that is, the ratios of the numbers of the tetraktys) "are in some way connected to the relationship existing between the whole numbers" (Plichta, p.191). What follows is an attempt to explain how the Pythagoreans made the connections between whole numbers, geometry, and the simple ratios of the monochord that led to the codification of the tonal system. I believe that there is a pattern to the organization of numbers, which serves as the basis for the tetraktys model and its application to cyclical processes. The evidence of this organizational principle comes from the fields of numerology, astrology, chemistry, physics, and in the prime number cross, a discovery of Plichta that I will describe in some detail below. The same pattern of organization appears again in the familiar form of the circle of fifths, as I will demonstrate. 
 
 

On the microcosmic level the organization of the enneagram, a number wheel that forms the basis of numerology and gematria ³⁾, is an application of the same basic tetraktys model that the Pythagoreans (or their predecessors in Babylon) applied to the planets. Among the theories that allegedly originated with Pythagorean thinking, numerology is a sort of academic black sheep. Science dismisses the concept of numerology as unscientific, based merely on superstition, and just plain nonsense. Today the average educated person would probably consider numbers to be nothing more than abstractions that have no meaning in and of themselves. The idea that numbers could have character and spiritual value of some sort seems ridiculous to the modern rational mind. Yet, even in the 21^st century, there are very few thirteenth floors in high-rise buildings and it is not hard to think of many other examples of relics of numerological thinking throughout the world. It is not my goal here to defend the legitimacy of numerology. Discovering more about the origin of numerology and its history would be a very interesting topic. But rather than enter into an extended investigation of the mystery of numbers, the focus here is on the enneagram which bears remarkable similarity to what I believe corresponds to the Pythagorean tetraktys model of the tonal system. Figure 2 is an example of the enneagram.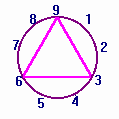 

Figure 2: The Enneagram.

Not surprisingly, this circular arrangement of numbers, while of unknown origin, is very likely an invention of the Pythagoreans. Apparently, numerologists and astrologers have known of this figure and its meanings and applications for over two thousand years. Modern numerologists use the enneagram to determine various aspects of a person’s character. Here are some significant features:

• Each number has certain personality characteristics associated with it. 

• Notice that the number 10, were it to be placed in the system, would line up over the number 1. I would like to suggest that the missing number 10 relates to the counter-earth, the unseen planet or perhaps, the fixed stars. The inner triangle hints at a link to the tetraktys.

• For numerologists numbers reduce to their corresponding mod 9 values, that is, any number is represented by its remainder after division by 9. For example, the number 11 is reduces to the number 2, the number 15 is 6, and the number 10 reduces to 1. 

In considering the third point, the number 10 connects to the number 1 by more than just the overlap; they relate to each other by reduction in mod 9. The practice of reducing a number to mod 9, also known as casting out nines, allows the expression of all whole numbers as single digit numbers. I will later discuss more about the significance of this feature. Another feature of the enneagram that I would also like to point out is that the position of the 9 coincides with the position of the number 0. 

It is interesting to note the relationship that this number wheel has to the clock face. Thinking of the clock face it is easy to understand how the numbers 8 and 1 are mirror opposites, just as 11 o’clock is the mirror of one o’clock with respect to twelve o’clock. I will discuss more about the clock face aspect of the enneagram later. 

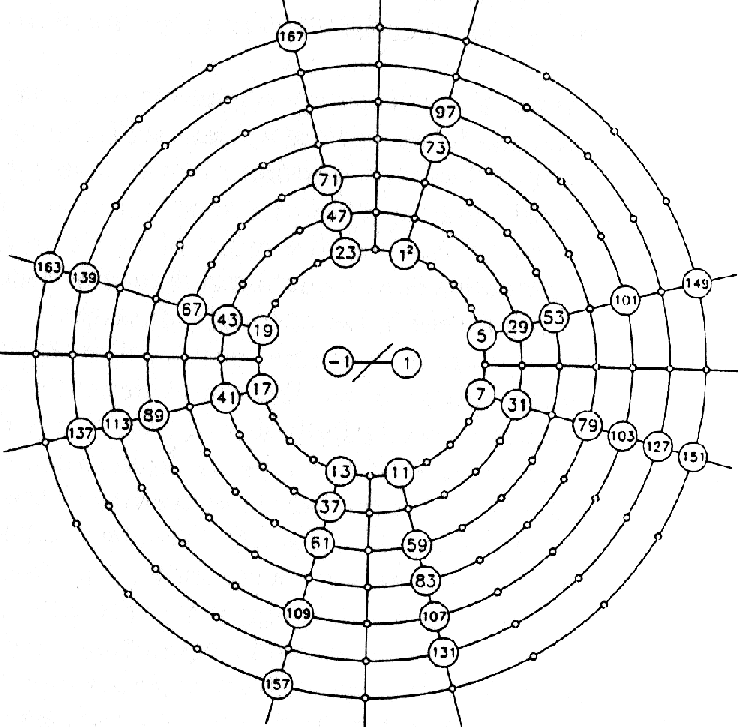
In spite of the fact that both numerology and the planetary model of Greek astronomy are perhaps spurious and unscientific, there may yet be a reasonable theory behind the models. Before presenting what I believe this theory is, I would like to discuss more of the ideas of German mathematician, chemist, and physicist, Dr. Peter Plichta.
 
 

Plichta’s book, God’s Secret Formula, is undoubtedly quite controversial and I am sure there is much resistance to his basic premise that invokes (or re-invokes!) the importance of number as the organizational principle of nature and attempts to debunk "big bang" theory and quantum mechanics in one fell swoop. From Plichta’s life-long study, he has come to believe that "at some time in the future the Pythagorean notion that everything is number and Kepler’s notion that everything is geometry would finally be accepted" (Plichta, p.142). In the book, Plichta constructs and demonstrates his prime number cross that is, basically, his model of the organization of the natural world. Plichta relates the cross to many aspects of the chemical periodic table, the structure of DNA, fractal geometry, pi, tonal music, and universal constants to the spatial organization of numbers. As with numerology, I am not here to defend the ideas of Plichta. Instead, I would like to offer his prime number cross as another example of the type of organizational principle that I believe is the essence of the Pythagorean tetraktys model for tonal music, which in turn is basically a form of the enneagram. Although Plichta covers many different aspects of the physical world, I will try to confine my discussion to his ideas about music. 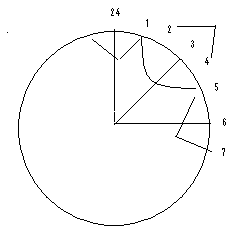Below is a diagram of Plichta’s prime number cross.

Plichta has organized his model around a property of prime numbers, that is, a prime number in this arrangement is located on either side of multiples of six: 

This property holds true for all the known prime numbers with the exception of the numbers 2 and 3. In the model there are eight rays emanating from the first circle aligned with prime numbers that lie in the first circle (5,7,11,13,17,19,23). A multiple of six lies in the rays between the prime number rays. The pattern for the prime numbers works for the pairs 5-7, 11-13, 17-19 but at 24, the prime pair is 23 and the non-prime number 25 (the square of the prime number 5). This is one reason why Plichta restarts the cycle such that 25 lines up with 1.

In Plichta’s analysis of the prime number cross he found that the circle of numbers contains only three basic categories of numbers derived from the first three whole numbers 1,2, and 3 ⁴⁾. This is because each quadrant of the circle is an isomorphic structure with 3 and its multiples as axes of symmetry. 

• This means that these three numbers are the basis of the entire structure of the number system.

• The number six is what Plichta calls the scaffold of the prime number cross since the prime numbers cluster around it. Six is also the sum and product of the first three numbers: 6 = 1+2+3 and 1*2*3. Six is also the first perfect number because of the fact that its sum and product are equal (28 is the next perfect number). 

• Eight is a structural number because of the eight prime number rays based on 1. In addition, there are eight rays for the numbers based on both two and three.

In an earlier drawing of the cross, the numbers –1, 0, and 1 are a part of the pairs of prime numbers. This group, -1,0,1 fit into the prime number property of six shown above leading Plichta to conclude that they belong in the cross and that –1,1 should be included as a prime number pair. The prime numbers belong with this –1,1 group and both are then prime numbers.

Plichta removes this group and places it in what he terms an inner shell, evoking a model very similar to the electron shells of atomic theory, which we see put back into the cross at their positions in Figure 3. Notice that the number 1 in the first outer is expressed as 1². Just why the 1² appears here is rather difficult to explain, but it can be considered the area of the space around an innermost circle, which surrounds zero ⁵⁾. Some other features of Plichta’s model are noteworthy: 

• The number twenty-four is a link to the tetraktys from the relationship mentioned above. (1*2*3*4, 4! = 24). Plichta points out that the twenty-four hour clock was an invention of the Egyptians who also introduced the decimal system to humankind, implying that they may have a common source of derivation, although he does not elaborate this point further. 

• Another central concept in his model is that the prime number cross is a model for matter, which exists in four-dimensional space. By his logic, three-dimensional shapes must exist in the context of a fourth dimension. If the prime number cross exists in two dimensions it is defined by an area which is the square of a number, Number space exists as two intersecting prime number crosses and is therefore defined as the square of the square of the area of a number, hence there are four dimensions to number space. Having established a four-dimensional space, he formulates the relationship between energy and time by stating that: "If matter did not exist…there would also be no space. But if only the two exist at the same time, then the one would have to be the other, only reversed. Where there is no movement, there also no time. Energy can therefore be nothing else but the reverse of time" (Plichta, p.130). 

• Plichta makes the claim that central to his model’s organization is the relationship of number to space. He emphasizes that there are two aspects to four-dimensional space, one of which, governed by the whole numbers, increases toward infinity, the other of which, governed by and simultaneous with the reciprocal of every whole number, decreases infinitely toward zero. If this is true, then the "infinity of space will exist reciprocally as points of matter" (Plichta p.130). This is an important point in understanding how music is organized. In a sense then the organization of nature by the whole numbers in the form of the prime number cross creates a simultaneous correspondence that follows the organization of the reciprocal of the whole numbers. Both types of space depend on the base numbers 1,2, and 3 and the "structural number" 8. The prime number cross spherically expands toward infinity as its reciprocal simultaneously contracts as an equilateral triangle toward zero.

Plichta’s thinking here definitely relates back to Pythagoras and his followers. The Pythagoreans understood the enigma of infinity and its reciprocal relationship to 0 ⁶⁾. The problem here is that the whole numbers increase indefinitely to infinity and, at the same time, their reciprocals can infinitely approach 0, yet logically, the distance between 0 and 1 must be the same as the distance between 1 and 2:

The number 1 then is a point of balance between the infinity of numbers (the macrocosm) and the infinity of zero (the microcosm). This relationship has a very simple, seemingly trivial, mathematical expression:

In mathematics, the hyberbola expresses the graph of the function of 1/X. Plichta points out that the shape of the hyperbola results from "the inversion of infinitely small sections of increasingly large circles" (Plichta, 176). It follows from the above expression (when we multiply both sides of it by X) that a number, X is related to its reciprocal by its square, the two-dimensional area. 

This equation, again seemingly trivial, is a link between a number and its reciprocal and it is a reflection of the relationship between 0 and infinity. If a number implies a space around itself, then the square of the number is meaningful in describing this space. This aspect of number theory relates to the Pythagorean fascination with the squares of numbers, reciprocals, and proportion. The latter two are central to the study of the monochord and to the theory of musical intervals. Starting with the open string of a given length, measurements that yield the various intervals are proportions of the string length. The ratios arise from the number of divisions made for a given string length. For example, 1:2 yields an octave relationship. Exactly one-half of the string length is twice the frequency of that of the total string length and the string divides into two equal parts. When you divide the string into three parts, the relation of the fifth (1/3 or 2/3), creates three equidistant increments in a 1:3 proportion to the original string length. We can see from this that at a very basic level there is a relationship between number, its reciprocal, and spatial increment created by the relationship. One can array numbers in a straight line or on a circle and the same incremental distribution almost seems to be an inherent property of the number system. In a sense, this seems true merely because numbers are just abstractions created by thought. Nonetheless, when we conceive of numbers there is an implicit evenness of value and distribution in the concept such that the distance from 0 to1 is equal to the distance from 1 to 2. The important conclusion that Plichta reaches is that "for each whole number the infinite reciprocal value also exists" (Plichta, p.191). 

From the idea of the simultaneous existence of a number and its reciprocal it follows that the coherence and precision of musical organization results both from the operations of the whole numbers and that of the reciprocal whole numbers. A musical note travels through space in the form of longitudinal waves, the result of billions of collisions of gas particles. Plichta demonstrates that the mechanism of control of the transmission of a musical note through space "could only be caused by the sequence of the reciprocal prime numbers" (Plichta, p.180). The sequence of the reciprocals of the prime numbers obeys a certain pattern that we find in fractal geometry. 

How does fractal geometry relate to the transmission of a musical note in space? Plichta applies probability theory to gas filled space and showing that the collisions of particles in a gas medium creates a distribution which follows a pattern that conforms to the numbers in Pascal’s triangle. The numbers in the triangle, referred to as Pascal numbers, emerge from binomial expansion in which the Pascal numbers are the coefficients of the expanded form of (a+b)ⁿ. For example, the first five rows shown below result from the following binomial expansions.
 

One may also generate the inner Pascal numbers in each row by adding the two numbers to the left and right of it in the row above. The pattern emerges as a result of billions of collisions of particles in a gas medium which reduce to yes/no decisions. Plichta compares the next diagram to a ball falling through successive rows of nails set up as a triangle. The numbers represent the probability of the path taken by a ball as it falls through from the top of the grid to the bottom. For example, at the very top, the ball will hit the first nail and go with equal probability to the right as to the left. This is why there is a 1 on the left and a 1 on the right at the second level. Going from level two to level three, there are two chances that the ball would fall to the middle because each possible outcome in level two has two more possible paths. 

The figure below is an expanded version that extends to the 65^th row.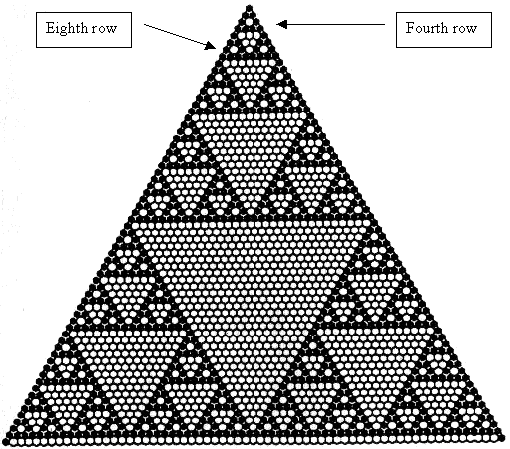

Figure 7: The Sierpinski Triangle.

The eighth stage of the Pascal triangle, with exponent value of seven, completes an isomorphic pattern that is reproduced in multiple copies at every subsequent eight levels (levels 16, 32, 40, 48…etc.) ⁷⁾. The Sierpinski triangle, shown above in Figure 6, contains the best illustration of the pattern. The white dots represent even Pascal numbers and the black dots are odd numbers. The Pascal triangle in Figure 6 occurs as the second totally black horizontal row (of eight) in Figure 7. Note that the triangle defined by the first black row of four is the tetraktys, itself an isomorphic component of the larger eight-row pattern. The structure of the tetraktys, governed by 2 and 3 (which are the two prime numbers that do not fit in the 6n ± 1), is the basis of the construction of the entire pattern at various hierarchical levels. Consequently, at every level of isomorphism the pattern architecture results from the organization of the prime numbers, especially the numbers 2,3, and 7. At every eighth row at least one new triangular pattern is restarted, which why 8 is a structural number in the Pascal triangle. 

For music, this is a rather concrete way of understanding the octave and why seven is a crucial number in the tonal system. This pattern within the Pascal geometry is the basis of fractal geometry. A voice or instrument transmits musical notes as sound waves that obey the fractal pattern seen above. 

I believe that Plichta has gone a long way toward explaining many aspects of tonal music. Many of his findings point back to knowledge that either originates with Pythagoras and his followers. It is also quite possible that the knowledge attributed to Pythagoras was actually from a more ancient source. Whatever the case, there can be no doubt that the tetraktys is much more than just some mystical symbol based on superstition as recent scholarship may lead us to believe. The Pythagoreans did find what appears to be a basic component of the structural organization of nature. From the evidence gathered above, I have formulated a basic model of how the tetraktys and its circular analogue, the enneagram, is a model of tonal theory. 
 
 

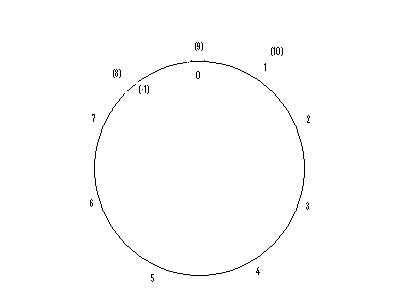
After examining the enneagram and the prime number cross, I found that both circular arrangements have one interesting common feature. Each arrangement lines up the numbers so that there is an overlap of three beginning numbers with the three numbers that start with the penultimate number. This is clearly demonstrated in Plechta’s model in which he actually puts three numbers in the center, -1, 0,1. These numbers correspond to 23, 24, and 1². I believe that the enneagram reflects the same overlapping procedure although it is not as apparent and the overlap seems to be accomplished differently. I think that in the enneagram the same overlap occurs, but it simply involves the last three numbers with the ten left out as it is subsumed with the number one in the mod 9 arithmetic. Furthermore, I believe that Plichta’s inner shell numbers do correspond to the first numbers in the Greek model, so that when the Greek start the tonal scale they are really starting with a third number. This suggests that the number group –1,0,1 descends from some original conception of the first three numbers that were not counted as actual numbers. I do not know whether the Pythagoreans thought of the inner circle in the same way that Plichta does, but the overall result is the same. 

Going back to the idea that a group of the first three numbers combine in the Pythagorean model, I offer the following model as the possible organizational principle of the tonal system, which shows how the tonal system is a model derived from the tetraktys:

The numbers 8, 9 and 10 are in parentheses to reflect the dual nature that they acquire by virtue of the system that allows for only seven different pitch names. The nine here therefore has two possible positions: it is the same as the ninth which corresponds to the compound second, just as the octave (8) is both a –1 and also corresponds to the compound prime. Comparing this model with the enneagram reveals that they are essentially similar, suggesting a common link to the tetraktys model. I show the "inner shell" numbers –1,0,1 to imply that they bear relationship to the three numbers greater than seven in the cycle. The "inner shell" numbers correspond to last three numbers of the spatial arrangement created when a group of numbers is arrayed in a circular pattern in a specific way:

• –1 corresponds to the number tied to the clock face mirror image of the first number (here 1=8: octave equivalence) 
• 0 corresponds to the modulus of the circular arrangement (here of course 9)
• 1 corresponds to the last number of the group (here of course, 10).

The three points above may simply seem to be self-fulfilling and circular (if you will excuse the term) reasoning, because I have found that this arrangement works for any sequence of numbers, that is to say that any clock face or circular organization of numbers seems to be based on this overlapping of three principle. This observation may have relevance to the relationship between rhythm and melody, a consideration I plan to study further. To illustrate the overlap of three principle in a related system, I now demonstrate the organization of the Circle of Fifths as another model constructed with this principle. 
 
 

Just about every musician in the western world is familiar with the Circle of Fifths. There are fifteen keys in the system, which is interesting because fifteen is the next triangular number after ten (1+2+3+4+5=15). Since there are only twelve different pitches in the Western system, there are just twelve major keys (and, of course twelve minor keys). There are six enharmonic keys C#-D^b , F#-G^b , and B-C^b . The overlap of three occurs in the enharmonic groups:
 
 

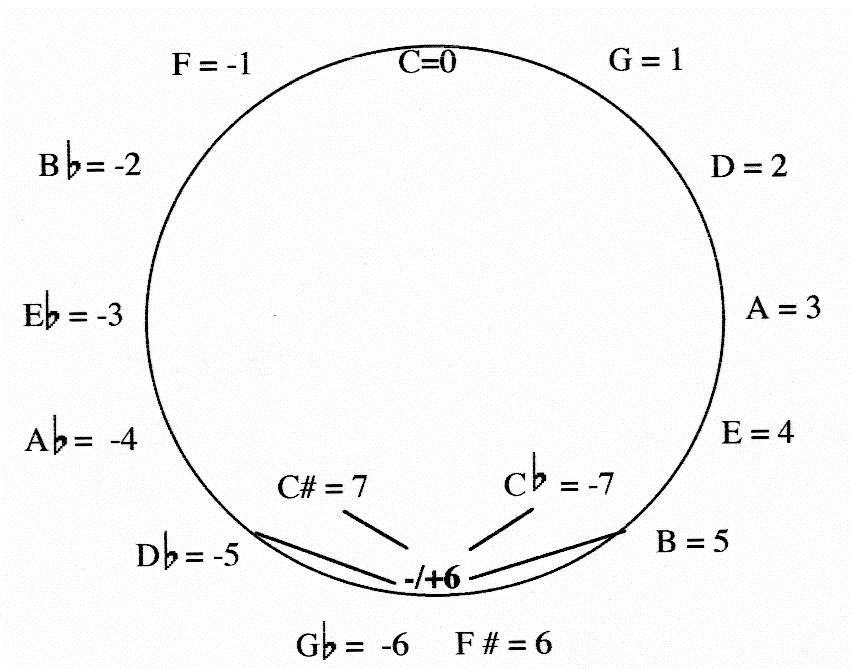
This yields the result that the twelve keys arranged in the circle of fifths align with overlap of three in this system that corresponds to the previous models. In this case, there is a double overlap resulting from the two sets of seven pitch names (plus the C (0)). When I began to think of flats and sharps as representing negative and positive values, I could then understand how the double overlap of three could occur. This system is basically the same number cycle organized around twelve different pitches, just as the tonal system is organized with seven. There are seven flat keys, seven sharp keys, and the "zero" key C.

It is interesting that, like Plichta’s inner shell of the prime number cross, there is a negative C a zero C and a positive C. I am not sure whether Johann Heinechen, believed to be the first to describe the Circle of Fifths in 1728, conceived of it in this way, however it seems remarkable that it is governed by the overlap of three and that it is based on the next triangular number, 15 (7+7+1). The overlap here surrounds the number six, instead of the number 0, showing that, when one arranges negative and positive values in a circle, the axis of overlap shifts to the penultimate number of the sequence. In effect, the negative end plugs into the positive end. Perhaps this explains Aristotles remark about the number three: 

Another curious fact to consider is that twenty-one sharp, natural, and flat pitches make up the total number of possible pitches in these fifteen keys, twenty one being the next triangular number (1+2+3+4+5+6). Whether this is merely a coincidence or just an artifact is an interesting question deserving of more study. 

The whole notion of number circles with of the overlap of three could well be of very ancient origin if the Ouroboros, the snake eating its own tail, is a symbol of this model as I suspect that it is. The overlap of three in a circular form does indeed suggest the metaphor of the mobilum perpetuum, the beginning and end as a cycle that is unending. It should not be surprising that we frequently find this almost universal symbol in alchemical texts. Figure 10 is an example of an Ouroboros from an ancient Greek alchemical text.

Figure 10: The Ouroboros (the inside caption reads: "The All Is One"). 

It would be difficult to prove whether this is true, but if it is, then the origin of music theory likely predates Pythagoras by a considerable amount of time. It is also intriguing that the clock face arrangement for number is somehow involved with sundial mathematics. The Egyptians and Greeks used a gnomon, originally the stick used for sundials, to figure the geometrically-shaped numbers. How these two things interact is lost to history. There seems to be much that has been lost, overlooked, or taken for granted where ancient knowledge is concerned.
 
 

I began this paper trying to answer the question: Why are there seven scale degrees in the major scale? The tetraktys model tells us that, when Pythagoras (or whoever it was who first described the tonal system) was thinking about the number seven; it was in relation to the number ten. The overlap of three principle is an easily demonstrable fact that automatically creates an organization of number in space. It is also such a simple notion that it is not so surprising that it was discovered a long time ago and that it seems to have been forgotten. I think that the most important concept that this circular model teaches us is that music is circular in nature. The circularity of music is not just metaphorical. It is to me a breath of fresh air to look at music from this viewpoint. Plichtas’ theory that time is the reverse of energy seems particularly applicable to describing the way music happens in time. His statement that "the human ear is specially constructed so that it registers fractal information transported through the air" (Plichta, p.191) is a thought provoking one that deserves further investigation. Music is the some of the best evidence there is that we have many new secrets to discover or rediscover about nature. The tonal system is an excellent example of the genius of the human spirit in its search to understand our relationship to this world.
 
 

Buckert, W.: Lore and Science in Ancient Pythagoreanism. (Cambridge, MA, Harvard University Press, 1972). 

Butler, C.: Number Symbolism. (London, Routledge & Kegan Paul, 1970).

Heath, T.: A History of Greek Mathematics. (New York, Dover Publications, Inc., 1981).

Hofman-Jablan, J.: Tonality/Atonality Order/Disorder or Order/New Order. Visual Math, 1, No.1, 1999.

Hopper, V. F.: Medieval Number Symbolism. (New York, Cooper Square Publishers, Inc., 1969).

Kingsley, P.:  Ancient Philosophy, Mystery, and Magic. (Oxford, Clarendon Press, 1995).

Kline, M.: Mathematical Thought from Ancient to Modern Times. (New York, Oxford University Press, 1972).

MacQueen, J.:  Numerology: Theory and Outline History of a Literary Mode. (Edinburgh, Edinburgh University Press, 1985).

Plichta, P.:  God’s Secret Formula. (Rockport, MA, Element Books, 1997).

Schimmel, A.:  The Mystery of Numbers. (New York, Oxford University Press, 1993).

Schrenk, L. P. : "God as Monad: The Philosophical Basis of Medieval Theological Numerology." in Medieval Numberology: A Book of Essays. Robert L. Surles, ed. (New York, Garland Publishing, Inc., 1993).

Shubnikov, A.V. and Koptsik, V.A.: Symetry in Art amd Science. (New York, Plenum Press, 1985).

Swetz, F. J. (ed.): From Five Fingers to Infinity. Peru, IL, Open Court Publishing Company, 1996). 

Uspenski, V.A.:  Pascal’s Triangle. (London, University of Chicago Press, 1974)
 
 

1)  Heath orders the ten spheres (emanating from the central fire and orbiting in a circle around it) counter-earth, earth, moon, sun, five planets (whose order he does not specify), and the fixed stars.  We can see in this organization the relic of the seven days of the week, though the days seem somewhat re-arranged. Eliminating the counter-earth, the earth, and the fixed stars, the days of the week (e.g. Monday = moon day) recall the planetary order though somewhat scrambled.  There are many different versions of the order of the planets, including ones that place the earth at the center instead of the ring of fire in the early model.

2) In fact, Heath states that Aristotle does offer other reasons for the existence of the counter-earth as a sort of explanation for certain types of eclipses (see Heath, p.165).

3) Gematria is the use of numbers assigned to letters of the alphabet to interpret the meanings of words.

4) Strictly speaking, the number 1 is really –1 and +1, but the square of both is 1, they reduce to one.

5) See Plichta, p.162.  It is also important to point out that, while 0 is left out in the inner level of prime number cross, it is still considered a part of the inner group.  There is also mention of an inner group of four numbers that are the root expressions of 1. Plichta uses Euler’s suggestion that the innermost circle, called the circle with radius, surrounds the number zero and contains the four root expressions of the number 1, -i,i,-1,1.  Though this may be somewhat unclear in the model, I still interpret that the inner shell contains three numbers, -1,0,1.  More research on Euler’s ideas concerning music is necessary. 
  
6) Zeno articulated many aspects of this with his four paradoxes.

7) It is interesting to note that the solid black lines in Sierpinski’s Triangle (Figure 6) occur at intervals that correspond to standard formal lengths of music (4,8,16,32,64).

8) From De Coel. I. :268 a 10.