Columns with Finite Symmetry -- Seven Types

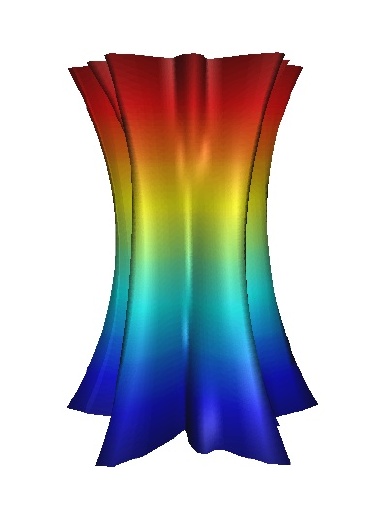
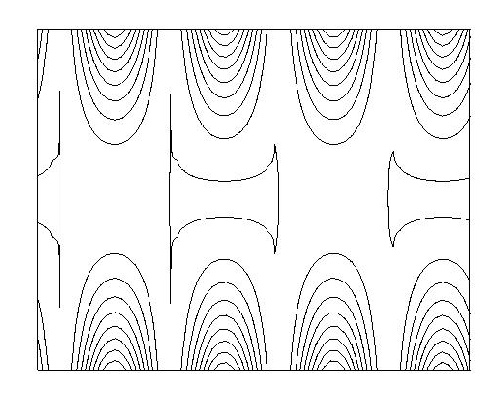
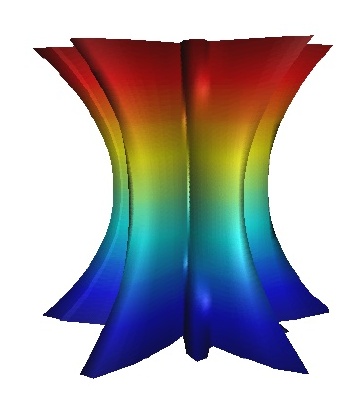
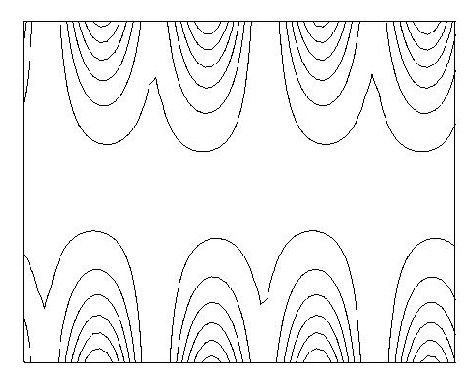
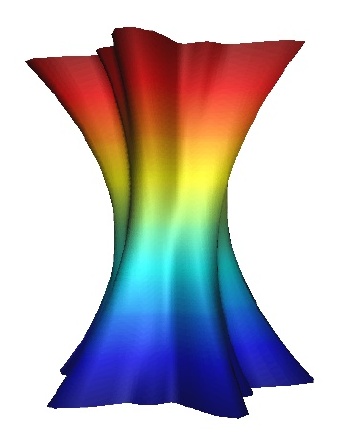
This types of column have neither a pure translation symmetry nor any symmetry that includes a translation symmetry. There are seven possible symmetry groups:

$${\bf 1} \quad <\kappa> \quad <\tilde{\kappa}> \quad <\tau\kap... ... \quad <\tau> \quad <\tau,\kappa> \quad <\tau,\tilde{\kappa}>.$$

An example of a column with no symmetry is given in Figure  23.Columns with just a single reflection or glide reflection are shown in Figure 24,  25, 26and  27, while columns with exactly two reflection or glide reflection symmetries are shown in Figure 28 and  29.

   

Figure 23:Column with no symmetries.

   

Figure 24:Column with up-down reflection.

   

Figure 25:Column with up-down glide reflection.

   

Figure 26:Column with left-right reflection.

   

Figure:Column with up-down rotation.

   

Figure 28:Column with up-down and left-right reflections.

   

Figure 29:Column with up-down glide reflection and left-right reflection.