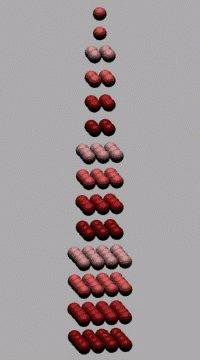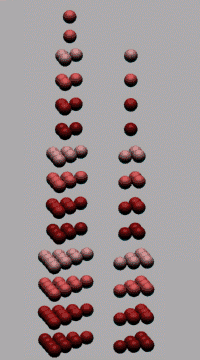In the Pascal's Triangle after a column of triangular numbers (two-dimensional space)  a column of  tetrahedral  numbers (three-dimensional space) follows. Let's make with our two-dimensional squares and triangles a similar transition. Let's build pyramids from them .

Figure 12. Transition from square and triangular numbers to pyramidal numbers (square pyramidal (square ground plan) and tetrahedral).

А) (on the left). The square pyramid consists of quartets of equal square modules (layers, stratums, storeys) except for the upper stratums of unit square, each of which contains only one unit (ball). Thus, from modules of one large pyramid it is possible to collect four small pyramids, two of which lack an apex as large as one ball (This peculiarity will be used in figure 27).

Besides, as it was noted,  the square number is equal to the sum of two triangular numbers. In our notation:  n= n + (n - 1).

Accordingly, square pyramidal (square ground plan) number is equal to the sum of two tetrahedral numbers:

 n = n+ (n - 1).

This feature will help us to express "volumes" in the pyramidal periodic table in terms of combinatorics using the Pascal's Triangle .

В) (On the right). The triangular pyramid consists of pairwise equal triangular modules, from which it is possible to build correspondingly two tetrahedrons.

The obtained figures can be considered as a set of modules, preparations for assembly of a 3D model of periodic system of chemical elements and its analogue (very general, primitive, not detailed) for atom nuclei. It would be more correct to speak about geometric images. These images help to understand the essence of the periodic phenomena in chemistry and nuclear physics, to look at these phenomena from the point of view of mathematics using concepts familiar to mankind during millenniums.

In the left pyramid it is easy to recognize the construction from the second modification of the Pascal's Triangle ! (Fig. 10). While working with different objects (the Pascal's Triangle and the table of electron shells filling) we came to one design – a pyramid.