|
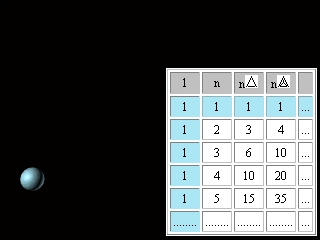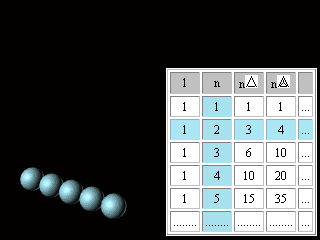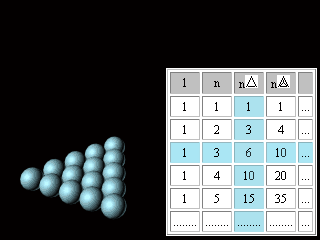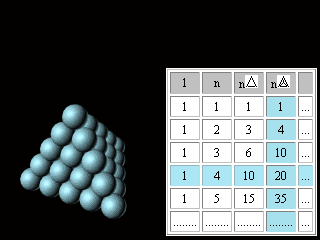
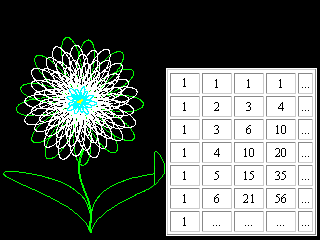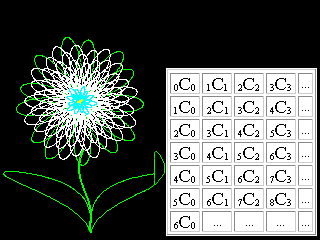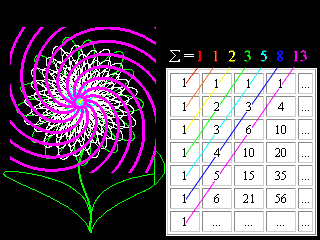
The peculiarity of the periodic system of elements offered below is, that the form is born as a result of certain operations with numbers and figures based on operations of symmetry. So the child playing with cubes (lego), creates architectural and other designs. An impulse for the present work was the find discovered at manipulations with the famous Pascal's Triangle*. (As I learnt later, such manipulations relate to the method of finite differences). *The Pascal triangle is an arrangement of numbers such that each number is the sum of two numbers immediately above it in the previous row. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1
The numbers can be
arranged a little differently. Let's turn (rotate) the array so that units
of one side of the triangle are posed in the first column, and units of
the second side of the triangle are posed in the first line of the table.
The table in the "rectangular" form was published in " Trattato di numeri et misure", 1556-60; ("Treatise on Numbers and Measures"), issued partially only after death of the author, which was outstanding Venetian mathematician Niccolo Tartaglia. The Pascal's Triangle appeared in the Blaise Pascal's work "Traitise du triangle arithmetique avec quelques autres petits traites sur la meme matiere" (written 1654, printed 1665 also after death of the author)[3].
Figure 7. Pascal's Triangle (Tartaglia's Table). Many patterns are found in the Triangle making it an intricate and complicated mathematical device. Some of them will be necessary for us. In columns and rows of the table starting from the second row we can find: natural numbers (n), figurate**: triangular (n(The signs used in this work for designation of figurate numbers are not common). ** Figurate numbers: Triangular numbers 1, 3, 6, 10, 15, 21, etc., were visualized as points or dots arranged in the shape of a triangle. Square numbers are the squares of natural numbers, such as 1, 4, 9, 16, 25, etc., and can be represented by square arrays of dots. Inspection reveals that the sum of any two adjacent triangular numbers is always a square number. Oblong numbers are the numbers of dots that can be placed in rows and columns in a rectangular array, each row containing one more dot than each column. An oblong number is formed by doubling any triangular number. The gnomons include all of the odd numbers; these can be represented by a right angle, or a carpenter's square. Gnomons were extremely useful to the Pythagoreans... Polygonal number series can also be added to form threedimensional figurate numbers; these sequences are called pyramidal numbers. (Britannica)
'... But the gentleman
dressed in white paper leaned
If Alice follows the advice, then with the equal price for travelling between stations the full amount paid for the tickets at each train stop will make the triangular numbers series. On the other hand the Pascal triangle contains
famous Fibonacci numbers (1, 1, 2, 3, 5, 8...), which have direct relation
to the phyllotaxis mentioned above.
Figure 8. Pascal's
Triangle, Fibonacci numbers and combinatorics. Fibonacci rows in
For combinations, k objects are selected from a set of n objects to produce subsets without ordering. The number of such subsets is denoted by nCk, read "n choose k." This is the same as the (n,
k) binomial coefficient.(Britannica)
|