|
Circle arrangements
Let us consider different plane arrangements of circles, where every intersection
or touching point is joint for exactly two circles. Any such arrangement is four-valent,
and by alternating it can be transformed into a projection of some knot or link.
For every circle arrangement we will consider the number of circles from which it consists
and the projection obtained. In the same way, we may consider the sphere arrangements,
and the arrangements of the corresponding circles. Obtained structures are modular,
because they originate from the set of the same basic elements - modules:
circles or spheres.
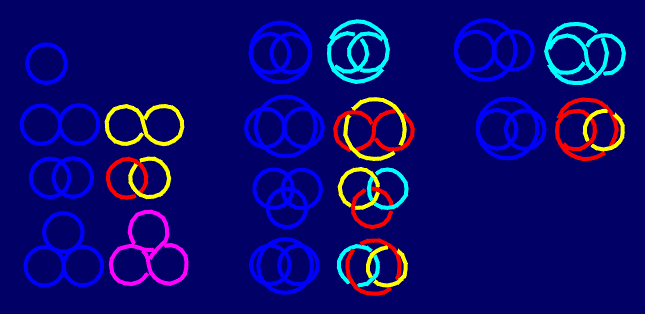














Different arrangements of circles may result in the isomorphic knot or link projections. For example, the first arrangement of three circles, and the other of four circles result in the same projection of the two-component link 512. 



In all the illustrated cases we used only circles touching one another from the outside. Some new possibilities, similar to certain "wasan"-patterns [14] arrise in the case of inscribed cicles. For example, except the "classical" Borromean rings (known also as one of Japaneze family crests), they can be derived from the following four-circle arrangement.


In the same way, from the Mon pattern (family crest) "Nine Stars" [15] we obtain the 16-crossing knot corresponding to 8-antiprismatic basic polyhedron. 
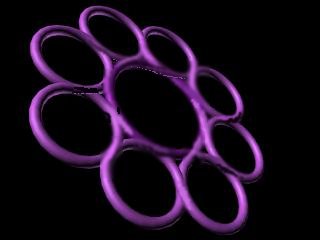
In the paper by prof. K.Husimi [16] we can find another interesting application: let us put on the tetrahedron surface three rubber rings all through the centers of the edges of the tetrahedron, alternating and forming Borromean rings. The string pattern printed that way on the plane by rolling tetrahedron will be so-called Kagome or woven bamboo pattern. The same traditional woven patterns are used by P.Gerdes for modelling the structure of Fullerenes [17]. 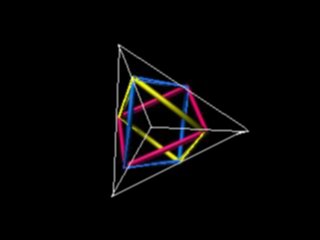

|