|
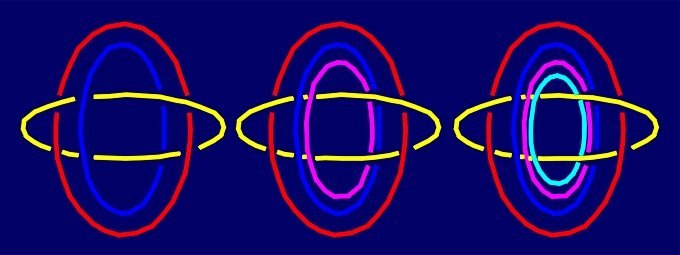
"Even" Borromean links
Next, we could try to construct Borromean links with an even number of
components and without the Brunnian property. C. Liang and K. Mislow
[8] proposed two methods for the construction of
n-Borromean links with at least one nontrivial sublink, by but
they both result in n-Borromean links with some nonintersecting
component projections (n>3). In the first method,
involving duplication of one or more rings, the duplicate rings
are interchangeable by continuous deformation. For example, by
duplicating one ring in Borromean rings, we obtain 4-Borromean link,
and continuing in the same manner, n-Borromean links (n=5,6,7…).
Different links of that infinite series follow from other choices of rings
that will be duplicated. |

|
Another method is similar to the one for producing "fractal" Borromean rings: in the trivial link, two crossing points are surrounded by nonintersecting circles. Continuing in this way, Borromean links with an even number of components are obtained. |
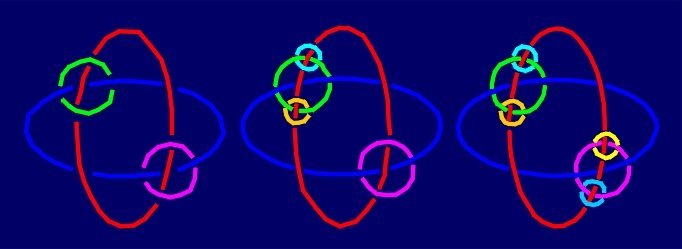
|
Finaly, only one open question remains: are they exist (2n)-Borromean links in which every pair of component projections has a crossing in all projections of the link, and moreover, where all components are equivalent. |